퀵 정렬(Quick Sort) 알고리즘

오늘은 퀵정렬(Quick Sort) 알고리즘에 대해 알아보겠습니다!

퀵정렬은 여러 정렬 알고리즘 중 하나로 이름에서도 알 수 있듯이 빠른(Quick) 속도를 보이는 알고리즘입니다!!

 

# 특징 

- 정렬 알고리즘

- 비교 정렬: 다른 원소와 비교를 통해 정렬 수행

- 1959년 토니 호어(Tony Hoare)에 의해 개발

- 분할 정복(Divide and Conquer) 방식

: 나열된 수를 두개로 분할하여 각각을 해결한 후, 결과를 모아서 원래 문제를 해결

# 동작 원리

퀵정렬을 한문장으로 정의하면 이렇게 표현할 수 있습니다!

"pivot 값을 선정해 해당 값을 기준으로 정렬하는 방식"

 

동작은 크게 3가지로 확인할 수 있는데욥 

1. 리스트(나열된 숫자)에서 기준값( = pivot) 선택

2. 기준값( = pivot)과 값을 비교하며  기준값( = pivot)보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 이동

3. 기준값( = pivot)을 제외한 왼쪽과 오른쪽 리스트(나열된 숫자)에 대해 (재귀적으로) 계속 반복

(더 이상 비교할 수가 존재하지 않을 시 종료)

 

### 기준값( = pivot) 선정 기준에 따라 다양한 방식이 존재함

EX)  random, 중앙값, 왼쪽 값, 오른쪽 값, 피벗2개 사용 등등

 

 

간단한 그림으로 도식화 해보았는데욥! 이와같이 나열된 리스트에서 기준값( = pivot)과 비교하며 작은수는 왼쪽, 큰수는 오른쪽으로 계속 분할하며 정렬되는 알고리즘입니다!!!

 

간단한 예제를 들어 확인해 보겠습니다!

예제 : 5, 3, 8, 4, 9, 1, 6, 2, 7

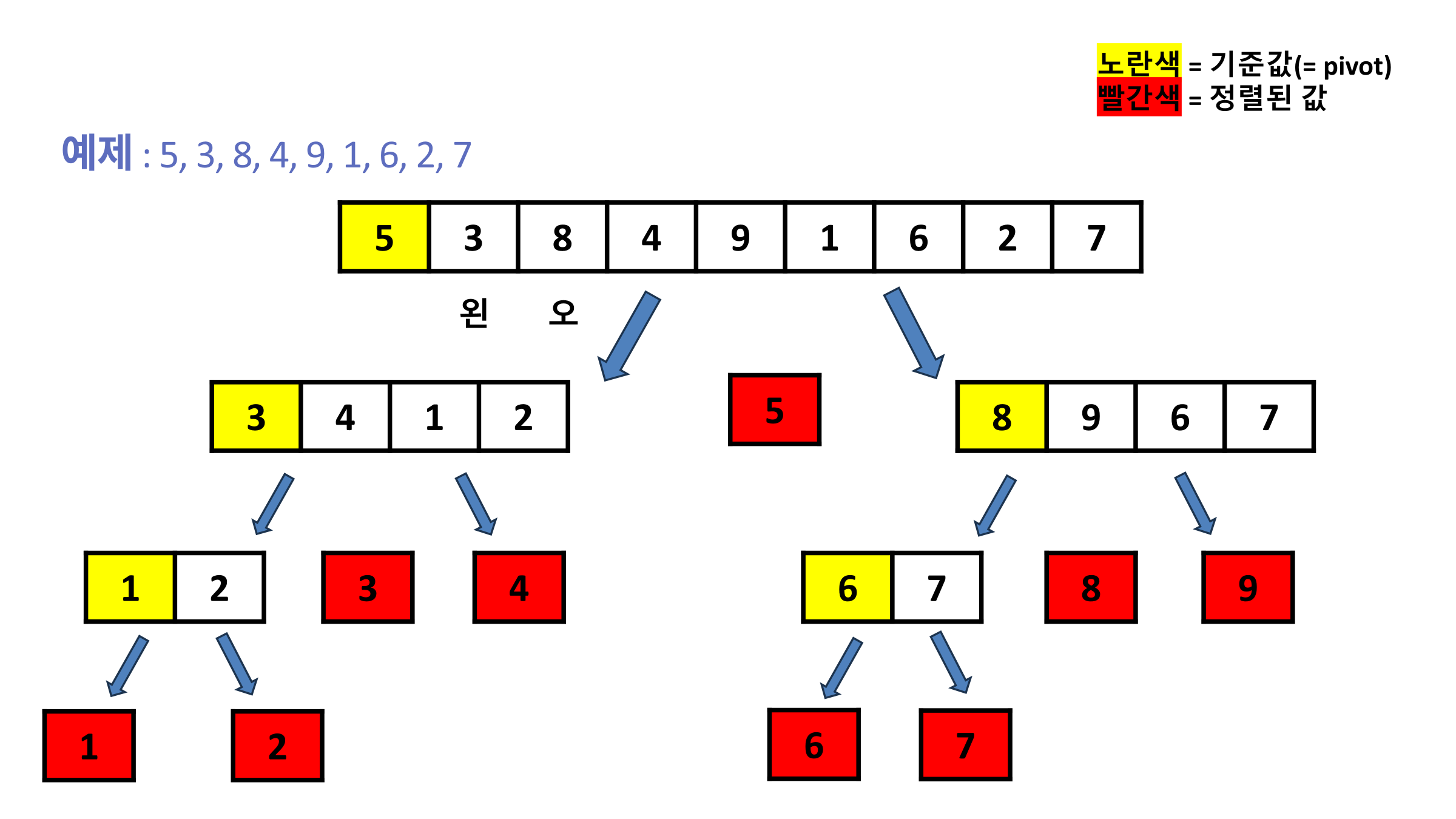
예제에서는 기준값( = pivot)을 제일 왼쪽 수로 선정하였는데욥 노란색이 설정한 기준값( = pivot)이며, 빨간색이 분할 후 빨간색을 의미합니다!

최초 5, 3, 8, 4, 9, 1, 6, 2, 7에서 기준값 5를 제외한후, 리스트를 순환하며 기준값보다 큰수는 왼쪽, 작은수는 오른쪽에 위치시키면 3,4,1,2 / 5 / 8,9,6,7 세 부분으로 분할됩니다

이 경우 5는 정렬이 완료된 상태이며 나머지 3,4,1,2 / 8,9,6,7 두 리스트에 대해서도 똑같이 기준값 선택, 리스트 순환을 진행합니다

분할된 부분이 더 이상 비교할 값이 없는 경우, 분할을 중지하며 해당 값은 정렬이 완료된 값이 됩니다!

최종적으로 정렬이 완료된 값(빨간색 값)을 나열하면 1,2,3,4,5,6,7,8,9로 오름차순 정렬이 완료됩니다

 

# Python 코드

1. 직관적으로 파이써닉하게 구현 - 추가공간 필요

def quickSort(x):    # x : List 형식 입력

    if len(x) <= 1:  # 분할된 요소가 1개 이하로 남을 시 종료

        return x

    pivot = x[0]    # 첫벗째 요소 피벗(기준값) 선택

    left, right, center = [], [], []

    for i in x:

        if i < pivot: # 피벗(기준값)보다 작다면 left

            left.append(i)

        elif i > pivot: # 피벗(기준값)보다 크다면 right

            right.append(i)

        else: # 피벗(기준값)과 같다면 center

            center.append(i)

    return quickSort(left) + center + quickSort(right)

 

pivot을 선택하는 다양한 방법을 적용할 수 있습니다!

-> 마지막을 피벗으로 선택 

pivot = x[-1]

 

-> 중앙값을 피벗으로 선택

mid_index = len(x) // 2

pivot = x[mid_index]  # 중간 요소를 피벗으로 선택

 

-> 랜덤값을 피벗으로 선택

import random

    pivot = random.choice(x)

 

+2개 피벗 사용 등등 다양한 전략들이 존재함

 

2. 구현이 복잡하지만 추가공간 거의 필요 없음

def quick_sort(A, left, right): # 최초 left = 0 (맨왼쪽인덱스)/ rignt = len(A)-1 (맨 오른쪽 인덱스)

    if left < right:  # 정렬 범위가 2개 이상인 경우

        pivot = partition(A, left, right)  # 피벗기준 좌우 분할

        quick_sort(A, left, pivot - 1)  # 왼쪽 부분리스트 퀵 정렬

        quick_sort(A, pivot + 1, right)  # 오른쪽 부분리스트 퀵 정렬

    return A

def partition(A, left, right):

    low = left + 1  # 왼쪽 부분 리스트의 인덱스 (증가방향) 젤 왼쪽은 피벗이므로 +1

    high = right  # 오른쪽 부분 리스트의 인덱스 (감소방향)

    pivot = A[left]  # 피벗 설정 (첫 번째 원소를 피벗으로)

    while low <= high:  # low와 high가 역전되지 않는 한 반복

        while low <= right and A[low] <= pivot:  # low를 오른쪽으로 이동 (피벗보다 큰 원소 찾기)

            low += 1

        while high >= left and A[high] > pivot:  # high를 왼쪽으로 이동 (피벗보다 작은 원소 찾기)

            high -= 1

        if low < high:  # 선택된 두 원소 교환

            A[low], A[high] = A[high], A[low]

    A[left], A[high] = A[high], A[left]  # 피벗과 high 위치 원소 교환 (피벗의 위치 확정)

    return high  # 피벗의 최종 위치 반환

 

### 주의할점 

        while low <= right and A[low] < pivot:  # low를 오른쪽으로 이동 (피벗보다 큰 원소 찾기)
            low += 1
        while high >= left and A[high] > pivot:  # high를 왼쪽으로 이동 (피벗보다 작은 원소 찾기)
            high -= 1

 

해당부분을 아래와 같이 표현시 동일한 값이 연속으로 등장할 경우 무한루프에 빠질 수 있습니다!!

반례) [2, 2, 3, 5, 6, 70]

pivot = 2 (첫 번째 원소)

low는 두 번째 2에서 멈춤 (A[low] = 2이므로)

high는 계속해서 오른쪽에서 왼쪽으로 이동하는데, A[high]가 모두 pivot보다 크거나 같아서 결국 pivot 위치까지 이동하게됨

해당 과정이 계속 반복되어 무한루프에 빠짐

 

# 성능분석 - 시간복잡도

시간복잡도는 3가지 종류가 있는데욥 1. 최선인 경우(Best)  2. 평균적인 경우(Average)  3. 최악의 경우(Worst)가 있습니다. 

1. 최선인 경우(Best) = O(n logn)
2. 평균적인 경우(Average) = O(n logn)
3. 최악의 경우(Worst) = O(𝑛^𝟐)

 

 

1. 최선인 경우(Best) = O(n logn)

퀵 정렬의 시간복잡도는 분할된 깊이와 비교연산의 곱으로 표현할 수 있는데욥!

최선의 경우에는 매번 절반 정도로 분할될 시 배열이 절반씩 나눠지므로 재귀 호출의 깊이가 얕아지고, 분할의 깊이가 제일 얕아집니다. 즉, 밑이 2인 logn으로 표현이 가능합니다!

각 분할에서의 비교 연산의 수는 매번 n번 씩 비교하게 되므로 

분할된 깊이 X 비교 연산수 = logn X n = O(n logn) 

 

2. 평균적인 경우(Average) = O(n logn)

평균적인 경우에는 재귀적인 식을 수학적으로 증명할 수 있습니다!

 

 

3. 최악의 경우(Worst) = O(𝑛^𝟐)

최악의 경우에는 이미 정렬이 되어 있는 경우에 정렬을 하는 상황인데욥!

오름차순으로 정렬된 경우 기준값을 처음/ 내림차순으로 정렬된 경우 기준값을 나중으로 지정할 시, 최악의 경우가 발생합니다!

매 분할마다 기준값을 기준으로 양쪽 두개의 리스트가 생겨야 하지만 최악의 경우에는 한쪽만 존재하게 됩니다

또한 분할마다 하나의 값이 정해지므로 모든 값을 정렬하기 위해서는 총 n개의 분할이 생겨야 하며,

각 분할에서의 비교 연산 수는 n이므로 

분할된 깊이 X 비교 연산수 = ∑(k-1) = n(n-1) / 2= O(𝑛^𝟐)

 

# 역설적인 동작

역설적으로 삽입정렬(insertion)은 정렬되어 있는 경우 정렬시 O(n)으로 빠른 속도를 보이지만, 퀵정렬(quick)은 정렬되어 있는 경우 O(𝑛^𝟐)의 느린 속도를 보입니다!!

책장 정리시 책이 잘 꽂혀 있는 상태에서 추가적으로 정리할 때, 더 빨리 정리할 수 있는 삽입정렬(insertion)이 더 인간의 직관에 더 맞는 정렬방법같네욯ㅎㅎㅎ

퀵정렬(quick)은 잘 꽂혀있는 책을 다시 어지럽힌 다음에 처음부터 다시 정리해야 더 빠른 속도를 낸다는 식인데 사실 직관에 반대되는 정렬방법이죠,,,

 

# 정렬 알고리즘 비교

다음은 대표적인 정렬 알고리즘의 시간복잡도를 비교한 표입니다!

퀵 정렬은 정렬 알고리즘 중에서도 뛰어난 성능을 보여줍니다!

 

# reference

컴퓨터 알고리즘. (2006). 대한민국: 도서출판 홍릉(홍릉과학출판사).

Baase, S., Van Gelder, A. (1999). Computer Algorithms: Introduction to Design and Analysis, 3rd Edition. 인도: Addison-Wesley.