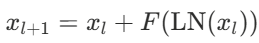Hippo's data
[Paper review] Pre-LN(Pre-Layer Normalization) 본문
트랜스포머 구조에서 오늘날 거의 표준으로 사용되는 Pre-LN(Pre-Layer Normalization) 구조에 관한 논문을 리뷰해보도록 하겠습니다!
Paper: On Layer Normalization in the Transformer Architecture
(Ruibin Xiong, Yunchang Yang, Di He, Kai Zheng, Shuxin Zheng, Chen Xing, Huishuai Zhang, Yanyan Lan, Liwei Wang, Tie-Yan Liu)
Conference: ICML 2020
ArXiv: https://arxiv.org/abs/2002.04745
On Layer Normalization in the Transformer Architecture
The Transformer is widely used in natural language processing tasks. To train a Transformer however, one usually needs a carefully designed learning rate warm-up stage, which is shown to be crucial to the final performance but will slow down the optimizati
arxiv.org
Pre-LN 최초 제안한 논문
Adaptive Input Representations for Neural Language Modeling(Alexei Baevski & Michael Auli, Facebook AI Research))
https://arxiv.org/abs/1809.10853
Adaptive Input Representations for Neural Language Modeling
We introduce adaptive input representations for neural language modeling which extend the adaptive softmax of Grave et al. (2017) to input representations of variable capacity. There are several choices on how to factorize the input and output layers, and
arxiv.org
ICLR 2019
On Layer Normalization in the Transformer Architecture
→ 기존 Post-LN의 한계점, 왜 Pre-LN이 좋은지 수학적으로 분석 (Post-LN VS Pre-LN)
1. SUMMARIZE
| 항목 | 핵심 내용 |
| Problem | Post-LN의 구조적 한계와 학습 비효율성 • Post-LN 구조: 출력층에 가까울수록 Gradient 크기가 커지는 경향이 있어 역전파 시 불안정함 • Warm-up 필수: 초기 Gradient 발산을 막기 위해 학습률을 0부터 천천히 올리는 Warm-up 단계가 강제됨 → 학습 시간 지연, 하이퍼파라미터 튜닝을 어렵게 함 |
| Method | Pre-LN 제안, Gradient 이론 증명 • 구조 변경: Layer Normalization(LN)을 잔차 연결(Residual Connection) 내부, 즉 Sub-layer(attention, FFN) 입력 전으로 이동 • 수식: • 이론적 근거: 테일러 전개(Taylor Expansion)를 통해 분석한 결과, Pre-LN은 층이 깊어져도 Gradient Norm이 일정하게 유지되어 Gradient Vanishing/Exploding 문제가 발생하지 않음을 수학적으로 증명 |
| Results | 학습 효율성 및 성능 최적화 • Warm-up 제거: Warm-up 단계 없이도 초기 학습이 안정적이며, 훨씬 높은 학습률(Learning Rate) 사용 가능 • 수렴 속도: 기존 대비 더 적은 반복(Iteration) 횟수로 동일 성능에 도달 (시간 단축) • 성능 검증: 기계 번역(IWSLT, WMT), BERT 학습 태스크에서 Post-LN과 동등하거나 더 우수한 성능을 보이면서 학습 비용은 절감 |
| Contribution | Deep Transformer 학습의 표준 정립 (Pre-LN ) • 기존 Post-LN에서 Warm-up이 필요했던 이유를 이론적으로 규명하고 해결책 제시 • 층을 매우 깊게 쌓아도 학습이 가능한 구조임을 입증하여, 이후 GPT-3, PaLM, Llama 2/3 등 현대 초거대 언어 모델들이 Pre-LN 방식 채택 |
2. DETAIL
1. Introduction

addition = Residual Connection
- (a) Post-LN(Layer Normalization) Transformer
- Layer Normalization가 Residual Connection(addition) 뒤에 위치
- 문제점: 평균장 이론을 통해 출력 레이어 근처 파라미터의 초기화 시점 예상 기울기가 크다는 것을 증명 (큰 기울기는 학습 불안정하게 함)
- 해결책: 학습률 웜업 단계(Learning Rate Warm-up Stage) 필요
- 모델 학습시, 학습률(learning rate)을 작은 값에서 시작하여 점진적으로 증가
- 작은 학습률로 시작 → 학습속도 늦어짐, 추가적인 하이퍼파라미터 튜닝 필요(Warm-up 정도, 최대 학습률 등)
- BERT, Original Transformer
- (b) Pre-LN(Layer Normalization) Transformer 제안
- Layer Normalization가 각 서브 레이어(Multi-Head Attention, FFN)의 입력 직전에 위치
- 학습률 웜업 단계(Learning Rate Warm-up Stage) 불필요
- 학습 시간 / 수렴 속도와 하이퍼파라미터 튜닝 노력 감소
- GPT 시리즈, LLaMA, PaLM
2. Related work
CNN, RNN → 초기 큰 학습률에서 점진적으로 감소
학습률 웜업 (Learning Rate Warm-up) → 큰 배치(batch) 훈련 시나리오, Transformer 선호
- 학습률 웜업단계 없다면, 최적화 발산 (optimization diverges)
3. Optimization for the Transformer
3.1. Transformer with Post-Layer Normalization
기존 트랜스포머 구조

Self-attention sub-layer
$Attention(Q, K, V) = \text{softmax}\left( \frac{QK^T}{\sqrt{d_k}} \right)V$
- 목적: 각 요소간 관련성 파악
- $Attention(Q, K, V)$
- 쿼리 (Query, Q): 다른 요소 탐색, 질의 주체
- 키 (Key, K): 각 요소들의 식별자 정보
- 값 (Value, V): 각 요소들의 실제 정보
- $\text{softmax}\left( \frac{QK^T}{\sqrt{d_k}} \right)V$
- $\mathbf{QK^T}$ (= 유사도 계산): 현재 요소의 쿼리(Q)와 시퀀스 내 모든 요소들의 키(K)를 곱하여(내적) 요소들 간의 유사도 점수를 계산 (얼마나 서로 관련이 있는지)
- $/ \sqrt{d_k}$ (=스케일링): 계산된 점수들을 히든 표현의 차원 크기 ( $\sqrt{d_k}$)로 나누어, 점수들이 너무 커지거나 작아지지 않도록 안정화 (학습 안정성)
- $\mathbf{\text{softmax}(\dots)}$ (=가중치 변환): 스케일링된 점수들에 소프트맥스 함수를 적용하여, 각 요소에 대한 최종 가중치(확률 분포)로 변환 (가중치는 현재 요소가 다른 요소들에게 부여하는 중요도를 나타냄)
- $\mathbf{(\dots)V}$ (=결합): 계산된 가중치들을 시퀀스 내 모든 요소들의 값(V)에 곱하고 합산 → 해당 요소는 관련성이 높은 다른 요소들의 정보를 효과적으로 결합하여 자신의 최종 표현을 업데이트함
멀티 헤드 어텐션(Multi-head Attention)
→ 어텐션 메커니즘 병렬 처리
$\text{Multi-head}(Q, K, V) = \text{Concat}(\text{head}_1, \dots, \text{head}_H)W^O$
$\text{head}_k = \text{Attention}(QW^Q_k, KW^K_k, VW^V_k)$
- $WkQ,WkK,WkV$: k개의 각 헤드는 입력 쿼리(Q), 키(K), 값(V)에 대해 가중치 행렬(학습 가능) 가짐
- $\text{head}_k = \text{Attention}(QW^Q_k, KW^K_k, VW^V_k)$: 각 헤드는 각각 어텐션 계산 수행
- $\text{Concat}(\text{head}_1, \dots, \text{head}_H)$: 각 헤드 출력을 결합
- $W^O$: 최종 선형변환 적용(각 헤드 정보들이 융합)
Position-wise FFN sub-layer
$FFN(h_i)=ReLU(h_iW^1+b_1)W^2+b^2$
- 목적: Attention 레이어 출력을 변환하여 각 위치의 벡터 표현에 추가적인 비선형성 제공
- $h_i$: i번째 벡터(토큰)
- 선형 변환 -> ReLU 활성화 -> 선형 변환
Residual connection and layer normalization
- Residual Connection
- 목적: 기울기 소실(vanishing gradient) 문제 완화 → 깊은 층에도 효율적 학습
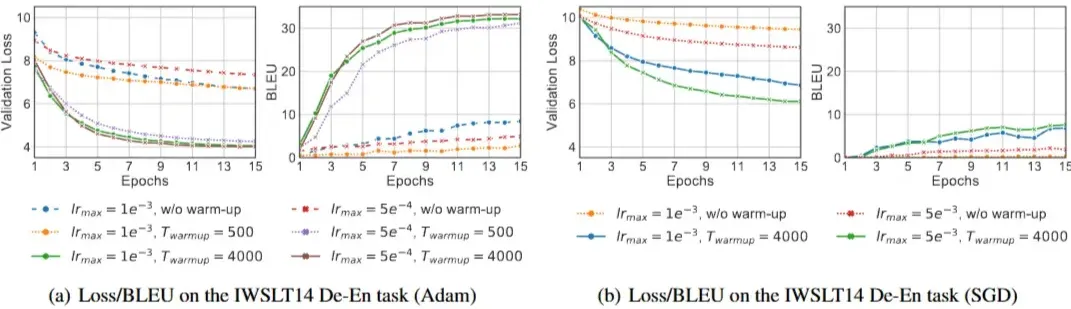
- x+F(x)
- sub-layer 입력(x)을 sub-layer 출력(F(x))에 직접 더함
- 잔차(residual) 변화를 학습하도록 함
- Layer Normalization (LN)
- 목적: 학습 과정에서 신경망의 활성화 값을 안정화하여 더 큰 학습률을 사용할 수 있게 함, 모델의 수렴 속도, 성능 향상
- LayerNorm(v)=$\gamma \frac{v - \mu}{\sigma} + \beta$
- 평균 $\mu = \frac{1}{d} \sum_{k=1}^{d} v_k$
- 표준편차 $\sigma = \sqrt{\frac{1}{d} \sum_{k=1}^{d} (v_k - \mu)^2}$
- $γ, β$: 학습 가능한(learnable) 파라미터
Post-LN Transformer
- Post-LN: LN이 각 서브 레이어(self-attention, FFN)의 출력과 잔여 연결이 합쳐진 후에 적용
- (기존 트랜스포머)
- Pre-LN: LN이 각 서브 레이어의 입력 전에 먼저 적용, 추가적인 최종 LN이 예측 전에 적용

3.2. The learning rate warm-up stage
다른 아키텍처들
- 큰 학습률(learning-rate)에서 점점 감소
- learning rate warm-up stage
- 작은 학습률로 시작하며 점점 커짐

- $lr(t)$: t번째 반복(iteration) 에서의 학습률
- t: 현재 훈련 반복 횟수
- $T_{warmup}$: 웜업 반복의 총 횟수
- $lr_{max}$: 웜업 단계가 끝날 때 도달하는 최대 학습률
- 웜업 단계 이후 → 일반적인 학습률 스케쥴러 적용(선형, 역제곱근 감소 등)
Experimental setting
- 목적
- 학습률 웜업 단계가 Post-LN 트랜스포머 훈련에 필수적인지
- 최종 모델 성능이 웜업 기간(Twarmup) 값에 얼마나 민감한지
- 실험 세팅
- 평가 지표: 검증 손실(Validation Loss), BLEU score
- 모델: Post-LN Transformer
- 훈련 중, 매 에폭마다 loss, BLEU 스코어 기록
| 💡 BLEU Score (Bilingual Evaluation Understudy Score) → 기계 번역(Machine Translation) 성능평가지표 → 기계가 번역한 문장이 사람이 번역한 정답(Reference)과 얼마나 비슷한가? $\text{BLEU} = \text{BP} \times \exp\left( \sum_{n=1}^{N} w_n \log p_n \right)$
|
Results and discussions
- 학습률 웜업 단계가 Post-LN 트랜스포머 훈련에 필수적
- 웜업 없음(w/o warm-up) 모델 성능 저조
- Post-LN 트랜스포머의 최종 모델 성능은 Twarmup 파라미터(웜업 기간) 에 매우 민감
- Twarmup 4000 → 500 (lrmax = $1e^{-3}$) 성능 크게 저하
- 웜업이 Adam과 SGD 모두에 도움 → 특정 옵티마이저에 국한된 것이 아닌, Post-LN 트랜스포머 자체의 불안정성 문제 시사
3.3. Understanding the Transformer at initialization
→ LN 위치의 차이가 초기화 시점의 기울기에 어떻게 영향을 미치는지를 분석
Post-LN Transformer VS Pre-LN Transformer
서브 레이어(sublayer): Attention, FFN
- Post-LN
- LN이 잔여 블록 바깥에 위치
- 즉, 서브 레이어의 출력과 입력에 잔여 연결이 적용된 후 LN이 적용
- $x_{l+1, i}^{\text{post}} = \text{LayerNorm}\Big( x_{l, i}^{\text{post}} + \text{SubLayer}(x_{l, i}^{\text{post}}) \Big)$
- Pre-LN
- LN이 잔여 블록 내부에 위치
- 비선형 변환 전에 적용, 예측 직전에 최종 계층 정규화가 추가
- $x_{l+1, i}^{\text{pre}} = x_{l, i}^{\text{pre}} + \text{SubLayer}\Big( \text{LayerNorm}(x_{l, i}^{\text{pre}}) \Big)$
요약
이론적 분석을 위한 단순화:
- 단일 헤드 어텐션: 복잡한 Multi-head 대신 Single-head 어텐션 가정
- 특정 가중치 초기화: Self-attention 서브 레이어의 가중치 행렬($W^Q, W^K$)을 0 행렬로 초기화
- 가우시안 입력: 입력 벡터 또한 동일한 가우시안 분포에서 샘플링 가정
초기화(initialization) 정의
→ 학습 시작 전, 각 신경망 가중치(Weight) 파라미터에 최초 값을 부여하는 것
→ 표준적인 초기화 값(무작위)을 썼을 때, 구조(LN, Layer Norm 위치)가 그래디언트 크기에 어떤 영향을 미치는가
- Post-LN (기존): 초기화된 가중치 값들이 Layer Norm을 통과하면서, 역전파될 때 그래디언트가 사라지지 않고 유지되거나 커짐 →학습률이 높으면 발산함
- Pre-LN (제안): 초기화된 가중치 값들이 층을 지날수록 커지는데(Norm 증가), Layer Norm이 이를 역으로 눌러주는 역할(Scaling Down)을 함 → 그래디언트가 안정됨→ 학습률이 높아도 수렴함
파라미터 초기화 설정 (Parameter Initialization)
일반적으로 Transformer 계층의 파라미터 행렬은 일반적으로 Xavier Initialization을 사용
행렬이 Xavier 초기화됨
분포: $W \sim N(0, \frac{2}{n_{in}+n_{out}})$
| 💡Xavier Initialization Paper: Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, NIPS 2010) 문제점: 모델 학습시, 초기 가중치 설정 중요
→ 각 레이어마다 입력 및 출력 뉴런 수($n_{in}$, $n_{out}$)를 고려하여 해당 레이어의 초기 가중치를 어느 정도로 설정할지 결정 방법: 각 레이어를 통과하는 활성화 값의 분산(variance)이 일정하게 유지 (입/출력의 분산이 같게)
|
분석 방법: 평균장 이론 (Mean Field Theory)
전체 뉴런에 대해 계산할 수 없음 → 평균장 이론을 사용하여 전체 뉴런의 통계값을 기반으로 근사하여 초기 학습이 잘 되는지 확인
| 💡평균장 이론(Mean Field Theory, MFT) → 물리학(통계역학)에서 시작 - 복잡하게 얽힌 수많은 입자들의 상호작용을 단순화하여 평균적인 하나의 장(Field)으로 근사하는 방법 → 거대한 신경망의 학습을 수학적으로 파악하기 위해 이용 |
Theoretical Findings - Gradients at Initialization
보조정리(Lemma 1,2,3)
→ 구체적인 증명은 논문 Appendix
- Lemma 1: ReLU 통과 이후 크기(Norm) 변화
활성화 함수 ReLU가 입력 데이터의 크기에 미치는 영향을 수학적으로 정의
→ 가우시안 분포 $N(0, \sigma^2 I_d)$를 따르는 입력 벡터 X가 ReLU를 통과하면, 그 크기(Norm)의 기댓값은 절반이 됨
$\mathbb{E}(|ReLU(X)|_2^2) = \frac{1}{2}\sigma^2 d$
기존 크기 $d \times \sigma^2$ → $\frac{1}{2} d \sigma^2$
- Lemma 2 : Forward Pass에서의 Hidden State 크기(Norm) 변화
→ 초기화(Initialization) 상태에서 데이터가 레이어를 통과할 때, Hidden State 벡터의 크기(Norm)가 어떻게 변하는지
- Post-LN (기존)
- $\mathbb{E}(|x_{l,i}^{post,5}|_2^2) = \frac{3}{2}d$
→ Residual Block을 거친 후 매번 Layer Norm(LN)으로 정규화
→ LN이 매번 크기를 잡아주기 때문에 층의 깊이($l$) 상관없이 기댓값이 일정하게 유지
- Pre-LN (제안)
- $(1 + \frac{l}{2})d \le \mathbb{E}(|x_{l,i}^{pre}|_2^2) \le (1 + \frac{3l}{2})d$
→ LN이 Residual Path 내부에 있어 값이 계속 누적
→ 층이 깊어질수록 값이 선형적으로 증가
- Lemma 3 : Backward Pass에서의 기울기 스케일링 효과
→ Layer Norm의 미분값(Jacobian)은 입력 벡터의 크기에 반비례
$|J_{LN}(x)|_2 = \mathcal{O}\left(\frac{\sqrt{d}}{|x|_2}\right)$
즉, 입력 x가 클수록, 역전파되는 그래디언트는 작아짐
결론 - Theorem 1: 왜 Pre-LN은 Warm-up이 필요 없는가?
→ 마지막 레이어($L$)의 그래디언트 확인 (다른 레이어는 논문 Appendix 참고)
연쇄법칙(Chain Rule) 이용
$\frac{\partial \mathcal{L}}{\partial W} = \underbrace{\frac{\partial \mathcal{L}}{\partial y}}{\text{(1) Loss Grad}} \times \underbrace{\frac{\partial y}{\partial x}}{\text{(2) LN Jacobian } (J_{LN})} \times \underbrace{\frac{\partial x}{\partial W}}_{\text{(3) Input Grad}}$
- Post-LN: 입력 크기가 상수이므로 그래디언트가 줄어들지 않고 크게 유지
$|\frac{\partial \mathcal{L}}{\partial W^{2,L}}|_F \le \mathcal{O}(d\sqrt{\ln d})$ (매우 큼)
즉, 초기 그래디언트 폭주를 막기 위해 아주 작은 학습률로 시작하는 **Warm-up이 필수**
| 📌Step A. Lemma 2 대입 $|x^{post}|_2 \approx \sqrt{\frac{3}{2}d} \approx \mathcal{O}(\sqrt{d})$ Step B. Lemma 3 대입 $|J_{LN}|_2 \approx \frac{\sqrt{d}}{|x^{post}|_2} \approx \frac{\sqrt{d}}{\sqrt{d}} \approx \mathbf{\mathcal{O}(1)}$ Step C. 최종 계산 $\left|\frac{\partial \mathcal{L}}{\partial W}\right|F \approx \underbrace{\mathcal{O}(1)}_{\text{Jacobian}} \times \mathcal{O}(d\sqrt{\ln d}) = \mathbf{\mathcal{O}(d\sqrt{\ln d})}$
|
- Pre-LN: 입력 크기가 깊이($L$)에 비례해 커지므로, LN이 그래디언트를 억제
$|\frac{\partial \mathcal{L}}{\partial W^{2,L}}|_F \le \mathcal{O}(d\sqrt{\frac{\ln d}{L}})$ (층이 깊을수록 안정됨)
즉, 그래디언트가 자동으로 관리되므로 **Warm-up 없이** 바로 높은 학습률로 **빠르게 학습 가능**
| 📌Step A. Lemma 2 대입 $|x^{pre}|_2 \approx \mathcal{O}(\sqrt{Ld})$ Step B. Lemma 3 대입 $|J_{LN}|_2 \approx \frac{\sqrt{d}}{|x^{pre}|_2} \approx \frac{\sqrt{d}}{\sqrt{Ld}} = \mathbf{\frac{1}{\sqrt{L}}}$ Step C. 최종 계산  |
3.4. Empirical verification of the theory and discussion
즉, 제시된 이론적 통찰이 실제 Transformer 훈련 시나리오와 일관됨
→ Pre-LN Transformer는 초기화 시 기울기가 잘 제어되므로 warm-up 단계 없이도 더 안정적인 훈련 가능
4. Experiments
→ Pre-LN Transformer가 학습률 웜업 단계 없이도 안정적으로 훈련될 수 있고 더 빠른 수렴 속도를 보이는지 확인
4.1. Experiment Settings
Machine Translation
- 작업
- IWSLT14 German-to-English(독일어 → 영어 번역)
- WMT14 English-to-German(영어 → 독일어 번역)
- 비교군
- Post-LN Transformer 학습 → Learning Rate Warm-up Stage 포함 유/무
- Pre-LN Transformer 학습 → Learning Rate Warm-up Stage 제거
Unsupervised Pre-training (BERT)
- 작업
- BERT 모델 사전학습
- BERT 모델→ MRPC(Microsoft Research Paraphrase Corpus) 데이터셋에 미세 조정
- BERT 모델→ RTE(Recognizing Textual Entailment) 데이터셋에 미세 조정
- 비교군
- Post-LN Transformer 학습 → Learning Rate Warm-up Stage 포함
- Pre-LN Transformer 학습 → Learning Rate Warm-up Stage 제거
4.2. Experiment Results
Machine Translation

→ Post-LN(웜없 O) vs Post-LN(웜업 X) vs Pre-LN(웜업X)
- Post-LN(웜업 X) vs Pre-LN(웜업X)
- Pre-LN(웜업 X)은 Post-LN(웜업 X)보다 압도적으로 우수한 성능
- Post-LN(웜업 O) vs Pre-LN(웜업X)
- Pre-LN(웜업 X)이 Post-LN(웜업 O)와 비슷한 최종 성능을 달성하면서도 훨씬 빠른 수렴 속도
즉, 웜업 없는 Pre-LN 이 Post-LN 웜업 있든 없든 더 빠른 수렴
Unsupervised Preㄴ-training (BERT)

→ 세가지 task 조건 (a,b,c) 에서 더 빠르고 낮은 손실 / 더 높은 정확도 달성
3. Discussion
Peri-LN (Peripheral Layer Normalization)
Paper: Peri-LN: Revisiting Normalization Layer in the Transformer Architecture
김정훈(Jeonghoon Kim, NAVER Cloud/KAIST), 이병찬(Byeongchan Lee, KAIST), 박천복(Cheonbok Park, NAVER Cloud)
https://arxiv.org/abs/2502.02732
Peri-LN: Revisiting Normalization Layer in the Transformer Architecture
Selecting a layer normalization (LN) strategy that stabilizes training and speeds convergence in Transformers remains difficult, even for today's large language models (LLM). We present a comprehensive analytical foundation for understanding how different
arxiv.org
(ICML 2025)
reference
https://clova.ai/tech-blog/흔들림-없는-안정성-peri-ln으로-학습-발산을-막다
CLOVA
하이퍼스케일 AI로 플랫폼 경쟁력을 강화하고 비즈니스 시너지를 확장합니다.
clova.ai
- Post-LN (기존 Transformer):
- 장점: 깊은 모델에서 성능 유지 (LN층이 뒤에 있으므로, 깊어져도 신호 크기가 일정하게 관리됨 = 성능 쥐어짜기)
- 단점: 학습 초기단계 학습률 웜업(Warm-up) 같은 조절이 필수적
- Pre-LN:
- 장점: 학습 초기에도 웜업(Warm-up) 과정 없이도 안정적으로 학습
- 단점: 층이 깊어질수록 출력값의 분산이 커져(선형 증가) 일부 성능 저하가 발생할 수 있음
→ 기존 방식들이 정규화 층(Layer Norm, LN)을 모듈의 앞(Pre)이나 뒤(Post) 중 한 곳에만 두는 것과 달리, Peri-LN은 서브 레이어(Attention, MLP)의 앞과 뒤 모두에 정규화를 적용
Peri-LN → 두 방식의 장점을 합친 효과 (웜업 없는 안정적인 학습 + 깊은 모델에서의 성능 유지 동시에 달성)
- RevIN (Reversible Instance Normalization) vs Pre-LN (Layer Norm)
- RevIN:
- 데이터 분포 안정화
- 모델 외부 (입력층 직후 & 출력층 직전)
-
- 학습 안정화
- 모델 내부 (각 Sub-layer 입력 전) Pre-LN
- RevIN:
'Paper review' 카테고리의 다른 글
| [Paper review] iTransformer (1) | 2026.02.04 |
|---|---|
| [Paper review] PatchTST (0) | 2026.01.30 |
| [Paper review] GAN(Generative Adversarial Nets) (0) | 2026.01.29 |
| [Paper review] DLinear (0) | 2026.01.12 |
| [Paper review] Prophet 톺아보기 (0) | 2025.12.07 |