Hippo's data
버블 정렬(Bubble sort) 알고리즘 본문
오늘은 정렬 알고리즘 중에 기초인 버블정렬(Bubble sort)(=거품정렬) 알고리즘에 대해 알아보겠습니다!
# 동작과정
두개의 수씩 차례대로 비교해나가는 식으로 정렬을 수행하는데욥! 두수씩 묶어 비교하는게 거품같지 않나요?!?!

아래는 거품정렬의 간단한 예시인데욥 4,3,5,1,2의 수를 오름차순으로 정렬하는 과정입니다
총 4번의 순회를 통해 정렬이 수행되며, 최초 순회시에는 마지막 값이 최댓값이 됩니다

# Python 코드
버블정렬은 코드 구현이 매우 쉽습니다!
for i in range(len(arr) - 1):
for j in range(len(arr) - i - 1):
if arr[j] > arr[j + 1]: # 비교 후 교환
arr[j], arr[j + 1] = arr[j + 1], arr[j]
개선된 코드 (교환 여부 기록하여 비교횟수 줄임) - 뒤쪽(큰값)부터 채워넣음
# 성능분석 - 시간복잡도
버블정렬의 시간복잡도는 3가지 종류가 있는데욥 1. 최선인 경우(Best) 2. 최악의 경우(Worst), 평균적인 경우(Average) = O(n²) 가 있습니다.
1. 최선인 경우(Best) = O(n)
2. 최악의 경우(Worst), 평균적인 경우(Average) = O(n²)
1. 최선인 경우(Best) = O(n)
버블 정렬의 최선의 경우는 이미 정렬된 상태를 의미합니다!
최초 순회에서 n-1번 비교를 통해 swap(교체)가 이루어 지지 않게 되고 정렬이 완료 되는데욥 즉 O(n)의 시간복잡도로 정렬이 가능합니다

이동횟수 = 0번
2. 최악의 경우(Worst), 평균적인 경우(Average) = O(n²)
최악의 경우와 평균적인 경우에는 O(n²)의 시간복잡도를 가지는데요
최악의 경우에는 정렬의 목적과 반대로 정렬되어 있는경우를 의미합니다!
평균적인 경우도 마찬가지로 무작위로 배치된 경우에도 거의 모든 순회를 수행하며 정렬이 이루어 지게 됩니다
각 순회마다 비교 횟수를 모두 더하면 아래와 같은데욥! 등차수열의 합으로 표현할 수 있습니다
(n-1) + (n-2) + (n-3) ⋯ + 2 + 1
= (n-1)n / 2
= O(n²)
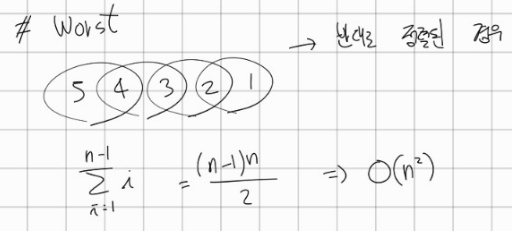
이동횟수 = 비교횟수 * 3
# 관련 문제
https://www.acmicpc.net/problem/1377
-> 버블정렬의 swap(교체)가 일어나지 않은 루프 출력
이 글은 ' Do it! 알고리즘 코딩 테스트 - 파이썬 편(김종관 저/이지스퍼블리싱 (주)) '를 참고하여 작성되었습니다
'Algorithm > 알고리즘 이론(Algorithm theory)' 카테고리의 다른 글
| 계수 정렬(Counting Sort) 알고리즘 (0) | 2024.11.11 |
|---|---|
| 기수 정렬(Radix sort) 알고리즘 (2) | 2024.11.11 |
| 삽입 정렬 (Insertion Sort) 알고리즘 (4) | 2024.11.09 |
| 선택 정렬 (Selection Sort) 알고리즘 (4) | 2024.11.09 |
| 퀵 정렬(Quick Sort) 알고리즘 (11) | 2024.11.01 |




