그래프 구현 with python

오늘은 그래프 구조를 구현하는 방법에 대해 알아보겠습니다

 

구현방법을 알아보기 전에, 먼저 그래프 구조 용어에 대해 간단히 알아보겠습니다!

# 그래프 구조 용어

그래프는 기본적으로 각 객체와 객체들을 연결하는 선으로 구성되어 있는데욥

 

객체: 노드(node), 정점(vertex)

선: 간선(edge), 링크(link)

선의 방향유무, 가중치 유무에 따라 여러 종류로 구분됩니다!

 

선의 방향 유무

방향 그래프 (Directed Graph) / 무방향 그래프 (Undirected Graph)

선의 가중치 유무

가중치 그래프 (Weighted Graph) / 비가중치 그래프 (Unweighted Graph)

이때, 가중치(weight)는 해결하고자 하는 문제의 시간, 비용, 거리 등등을 의미합니다!!

학부수준에서는 가중치가 (+)인 경우를 위주로 배우지만 (-)인 경우도 존재합니다

예) 비행기 비용 계산시, 위험 노선 테스트로 오히려 돈받고 타는 경우,,, 

 

# 그렇다면 그래프 구조가 필요한 이유는 무엇일까요?

바로 일상의 복잡한 문제를 그래프로 표현하여 단순화할 수 있기 때문입니다

예) 최저비용으로 비행기로 이동, 최단시간에 이동, 최적 하수도 시설, 최적 선로위치, Neural network, 코드 디버깅 등등

 

이제 본격적으로  그래프 구조 구현 3가지 방법에 대해 알아보겠습니다!

# 그래프 구조 구현 3가지 방법

 

1. 에지 리스트 (Edge List)

2. 인접 행렬 (Adjacency Matrix)

3. 인접 리스트 (Adjacency List)

 

1. 에지 리스트 (Edge List)

에지 리스트는 에지(간선)을 중심으로 표현하는 방법인데욥

노드와 노드간의 연결정보, 가중치를 튜플로 묶어 리스트에 저장합니다

 

- 가중치 X

(출발노드, 도착노드)

edge_list = [(1, 2), (1, 3), (3, 5), (3, 4)]

 

- 가중치 O

(출발노드, 도착노드, 가중치)

edge_list = [(1, 2, 7), (1, 3, 8), (3, 5, 1), (3, 4, 3)]

 

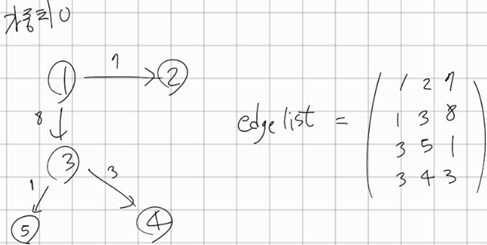
특정 노드와 연결된 이웃 노드를 찾을 시, 모든 간선을 확인해야 하므로 인접행렬, 인접 리스트에 비해 비효율적

주로이용: 벨만-포드(노드사이 최단거리), 크루스칼Kruskal( MST-최소신장트리찾기)

 

 

2. 인접 행렬 (Adjacency Matrix)

2차원 배열을 사용하는데욥 행, 열은 각각 출발노드, 도착노드가 되며 값은 에지(edge) 여부 혹은 가중치를 의미합니다

특히 에지 리스트는 간선 중심인 반면, 인접 행렬은 노드중심으로 그래프를 표현합니다

 

- 가중치 X

2차원 배열 값에  노드 간의 연결 여부 입력(연결:1 / 비연결:0)

n = 5  # 노드의 개수

graph = [[0 for col in range(n)] for row in range(n)] # 빈 2차원 리스트 생성

# 2차원 리스트 각 값 채우기

graph[0][1] = 1

graph[0][2] = 1

graph[2][3] = 1

graph[2][4] = 1

 

- 가중치 O

2차원 배열 값에  가중치 입력

n = 5  # 노드의 개수

graph = [[0 for col in range(n)] for row in range(n)] # 빈 2차원 리스트 생성

# 2차원 리스트 각 값 채우기

graph[0][1] = 7

graph[0][2] = 8

graph[2][3] = 3

graph[2][4] = 1

 

 

2차원 배열을 이용하여 매우 직관적으로 구현이 가능하지만, 노드와 관련된 에지(edge) 탐색시 N번 접근해야하므로 시간복잡도 비효율적(인접리스트보다 느림)

에지가 적을 시(희소그래프=sparse graph), 공간적으로 비효율적(2차원 배열에 채워진 값이 거의 없음)

 

 

3. 인접 리스트 (Adjacency List)

각 노드에 연결된 다른 노드들을 저장하는데요

파이썬의 딕셔너리와 리스트 구조를 이용하여 구현할 수 있습니다

 

- 가중치 X

 

딕셔너리 이용

graph = {

    1: [2, 3],  # 노드 1은 노드 2, 3과 연결

    2: [],    

    3: [4, 5],  # 노드 3은 노드 4, 5와 연결

    4: [],      

    5: []      

}

 

리스트 이용

graph = [

    [],         # 인덱스 0은 사용하지 않음 (0부터 시작)

    [2, 3],     # 노드 1은 노드 2, 3과 연결

    [],        

    [4, 5],     # 노드 3은 노드 4, 5와 연결

    [],        

    []          

]

 

- 가중치 O

 

딕셔너리 이용 - 도착노드: 가중치 (key:value)

graph = {

    1: {2: 7, 3: 8},  # 노드 1에서 노드 2로 가중치 7, 노드 3으로 가중치 8

    2: {},            

    3: {4: 3, 5: 1},  # 노드 3에서 노드 4로 가중치 3, 노드 5로 가중치 1

    4: {},            

    5: {}            

}

 

리스트 이용 - 가중치는 튜플로 저장

graph = [

    [],               # 인덱스 0은 사용하지 않음 (0부터 시작)

    [(2, 7), (3, 8)], # 노드 1은 노드 2로 가중치 7, 노드 3으로 가중치 8

    [],        

    [(4, 3), (5, 1)], # 노드 3은 노드 4로 가중치 3, 노드 5로 가중치 1

    [],              

    []                

]

 

구현은 복잡하지만, 노드와 엣지 탐색 시간은 매우 빠름

공간효율 좋음

실제 코딩테스트에서 주로 사용됨

 

# reference

이것이 취업을 위한 코딩 테스트다 with 파이썬. (2020). (n.p.): 한빛미디어.

파이썬 자료구조와 알고리즘: for beginner. (2021). 대한민국: 한빛아카데미.