퀵 선택(Quick selct) 알고리즘

안녕하세욥 오늘은 선택 문제(Selection Problem) 의 해결방법 중 하나인 퀵 선택(Quick selct)에 대해 알아겠습니다!

 

# 선택 문제(Selection Problem) 란?

선택 문제(Selection Problem)는 특정 순위의 요소를 찾는 문제인데요

 k번째로 작은(또는 큰) 요소를 찾는 문제입니다!

 

지금까지 포스팅한 정렬(sort)는 일정한 순서(오름차순, 내림차순 등)로 요소를 정리하는 방법이었는데욥

선택 문제(Selection Problem)도 정렬(sort) 후, k번째 수를 찾으면 되지만 지금까지 알아본 비교정렬의 특성상 아무리 빨라도 O(nlogn)의 시간복잡도가 필요하기 때문에 해당 선택 문제(Selection Problem)는 O(nlogn)의 시간복잡도가 필요하게 됩니다

 

## 비교정렬이 아무리 빨라도 O(nlogn)인 이유

https://hipposdata.tistory.com/105

비교정렬 시간 성능의 하한(lower bound): O(nlogn)

 

반면, 정렬(sort) 하지 않고 선택할 수 있는 방법들도 존재하는데욥

해당 경우 O(n)의 선형시간(Linear time)으로 선택할 수 있는 알고리즘들이 있습니다!

 

여러 선택 문제(Selection Problem) 알고리즘들이 있는데욥 오늘은 퀵 정렬(Quick sort)과 유사한 퀵 선택(Quick selct)에 대해 알아보겠습니다

 

## 퀵정렬(Quick sort) 복습

https://hipposdata.tistory.com/103

퀵 정렬(Quick Sort) 알고리즘

 

# 동작 원리

퀵 선택(Quick selct)의 동작은 퀵 정렬(Quick sort)과 거의 유사한데요

pivot값을 기준으로 분할하며 정렬해나가는 큰 틀은 동일합니다!

하지만 한가지 다른 점이 있는데욥

퀵정렬은 정렬하기 위해 분할된 부분을 모두 재귀적으로 반복하지만,

퀵선택은 분할된 부분에서 찾을 k번째 요소가 있는 부분만 재귀적으로 반복하여 탐색합니다!!

 

동작은 크게 3가지로 확인할 수 있는데욥 

1. 리스트(나열된 숫자)에서 기준값( = pivot) 선택

2. 기준값( = pivot)과 값을 비교하며  기준값( = pivot)보다 작은 값은 왼쪽, 큰 값은 오른쪽으로 이동

3. 기준값( = pivot)과 k가 동일 -> 종료 /

기준값( = pivot)의 인덱스가 k보다 큼 -> 왼쪽부분 재귀적 탐색 / 

기준값( = pivot)의 인덱스가 k보다 작음 -> 오른쪽부분 재귀적 탐색 /

 

5,3,8,4,9,1,6,2,7 에서 3번째로 작은수(k=3)를 찾는 과정을 예시로 표현해 보겠습니다 

 

 

# Python 코드

def quickSelect(x, k):  # x: 리스트, k: 찾고자 하는 수의 순위(k번째로작은)

    if len(x) == 1:

        return x[0]

    pivot = x[0] #  첫벗째 요소 피벗(기준값) 선택

    left = [i for i in x if i < pivot]

    center = [i for i in x if i == pivot]

    right = [i for i in x if i > pivot]

    if k < len(left):  # k번째 작은 값이 left 부분에 있는 경우 재귀적 반복

        return quickSelect(left, k)

    elif k < len(left) + len(center):  # k번째 작은 값이 center에 있는 경우

        return center[0]

    else:  # k번째 작은 값이 right 부분에 있는 경우 재귀적 반복

        return quickSelect(right, k - len(left) - len(center))

 

 

# 성능분석 - 시간복잡도

퀵선택은 퀵정렬과는 다르게 전체를 정렬하지 않고도 k번째 요소를 반환하므로 퀵정렬의 평균 시간복잡도인 O(nlogn)보다 빠른 성능을 보여줍니다!

 

1. 최선인 경우(Best) = O(n)

찾으려는 k번째 요소가 pivot일시, 1번의 분할과정만으로 찾기 때문에 O(n)의 시간복잡도를 가집니다!

 

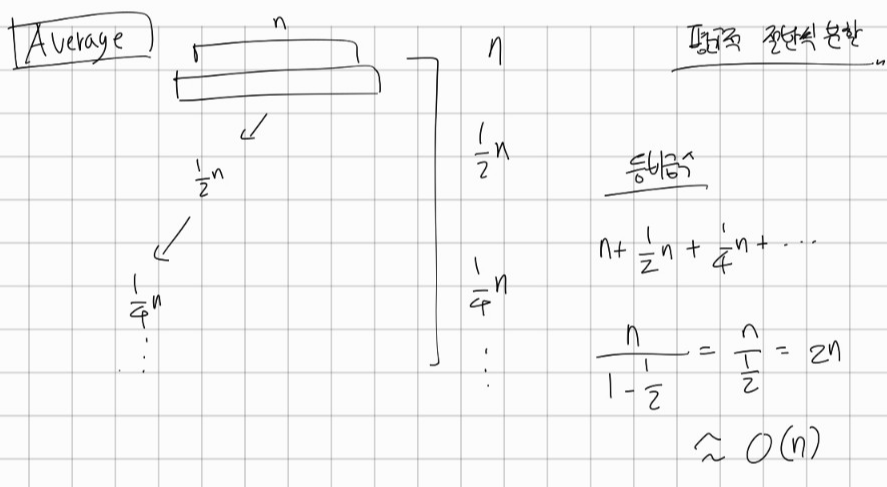
2. 평균적인 경우(Average) = O(n)

대략적으로 절반씩 분할되어 탐색된다고 하면, 무한등비급수로 표현할 수 있는데욥!

n+1/2n+1/4n + ...

= 2n 

즉, O(n)

 

3. 최악의 경우(Worst) = O(𝑛^𝟐)

최악의 경우는 퀵정렬과 동일한데욥 

피벗 선택이 매 단계마다 가장 비효율적으로 이루어져, 분할이 한쪽으로 치우쳐지는 경우입니다!

(총 분할된 깊이 n) X (n개의 배열) = n^2

즉, O(𝑛^𝟐)

# reference

https://www.youtube.com/watch?v=n4zBdbVaMgE