Hippo's data
소수 찾기 - 에라토스테네스의 체 본문
오늘은 소수 찾기 알고리즘에 대해 포스팅 하겠다!!
소수란 무엇일까?
자연수를 분류하자면 1, 소수, 합성수로 나뉜다.
소수(prime number) = 약수로 1과 자기자신만을 가지는 수 = 약수를 2개만 가지는 수
예) 2,3,5,7,9 ...
-> 1과 자기자신을 제외한 자연수로 나누어 떨어지지 않음
합성수(composition number) = 약수로 1과 자기자신 이외의 수를 가지는 수 = 약수를 3개 이상 가지는 수
예) 4,6,8,10 ...
소수 찾기를 간단한 코드로 구현하면
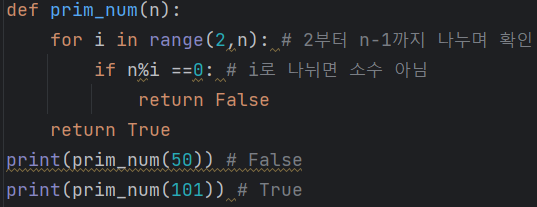
시간복잡도는 약 O(n)을 가지게 된다
즉, 소수를 찾을 때 약 n번을 나누며 확인해야 하므로 시간복잡도가 클 수 있다
이를 보완한 방법이
에라토스테네스의 체(Eratosthenes' Sieve)이다.
# 에라토스테네스의 체(Eratosthenes' Sieve)란?
고대 그리스 수학자인 에라토스 테네스가 개발한 알고리즘으로 체(필터)를 거르며 주어진 범위 내의 모든 소수를 효율적으로 찾을 수 있다.
1. 2부터 시작해서 숫자를 √n까지 하나씩 증가시키며 소수를 찾음
2. 현재 숫자가 소수일 경우, 그 숫자의 배수를 모두 지움
3. 모든 숫자에 대해 이를 반복 하면 남은 숫자는 소수가 됨
# √n까지 확인하는 이유
어떤 수 n = p X q 라고 가정
p가 √n보다 크다면 자동으로 q는 √n보다 작아져야 함
즉, n까지의 숫자 중 중간부분인 √n까지만 확인하면 √n보다 큰 수는 이미 제거 됨
예) 15까지 숫자중 소수 찾기


즉, 15까지의 소수 => 2,3,5,7,11,13 => 6개
해당 숫자 이내의 소수 찾기를 코드로 구현하면

시간 복잡도는 O(√n + n log log n)
n log log n이 더 큰 영향을 끼치므로 -> O(n log log n)
에라토스 테네스의 체를 이용하면 시간복잡도를 줄이며 소수를 찾을 수 있다
# 관련문제
https://www.acmicpc.net/problem/2960
'Algorithm' 카테고리의 다른 글
| 코린이의 백준 장학금 도전기 - 5주차(마지막 주차) (3) | 2023.08.27 |
|---|---|
| 코린이의 백준 장학금 도전기 - 4주차 (0) | 2023.08.19 |
| 코린이의 백준 장학금 도전기 - 3주차 (3) | 2023.08.12 |
| 유클리드 호제법 - 최대공약수GCD, 최소공배수LCM 구하기 (0) | 2023.08.08 |
| 코린이의 백준 장학금 도전기 - 2주차 (0) | 2023.08.05 |




