ch2지도학습_분류classification의 선형모델 linear_model

오늘은 저번에 이어서 지도학습 중 선형모델에 대해 알아보겠습니다

 

저번에는 회귀방식의 선형모델을 알아보았는데요

이번에는 분류 방식의 선형모델 실습을 해보도록 하겠습니다

 

분류용 선형모델은 이진분류Binary Classification와 다중분류Multiclass Classification로 구분할 수 있습니다

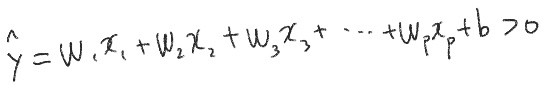
-> 임계치 0과 비교하여 방정식 값이 0보다 작으면 -1 / 크면 +1로 예측

 

 대중적인 알고리즘 

-> 로지스틱회귀 logistic regression / linear_model.LogisticRegression에 구현됨

-> 서포트 벡터 머신 support vector machine / svm.LinearSVC에 구현됨 

 

*** 주의) 로지스틱회귀 logistic regression -> 회귀 regression 이름이 들어가지만 분류알고리즘

 

# 이진분류 Binary Classification

from sklearn.linear_model import LogisticRegression

from sklearn.svm import LinearSVC

X, y = mglearn.datasets.make_forge()

fig, axes = plt.subplots(1, 2, figsize=(10, 3))

for model, ax in zip([LinearSVC(max_iter=5000), LogisticRegression()], axes):

    clf = model.fit(X, y)

    mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5,

                                    ax=ax, alpha=.7)

    mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)

    ax.set_title(clf.__class__.__name__)

    ax.set_xlabel("특성 0")

    ax.set_ylabel("특성 1")

axes[0].legend()

plt.show()

-> forge데이터 셋 사용 / LinearSVC, LogisticRegression 적용
-> 두모델 비슷한 결정경계만듦 / 똑같이 두개 데이터 잘못분류
-> 두모델 모두 기본적으로 L2규제 사용함 -> 규제강도 매개변수 : C(기본값 1.0)

mglearn.plots.plot_linear_svc_regularization()

-> C 커지면 규제 감소(모델복잡도 증가) = 훈련세트 학습 많이함 / 개개의 데이터 포인트 정확히 분류하려함(특정 데이터)
-> C 작아지면 규제 증가(모델복잡도 감소) = W가중치값 0에 가까워지게함 / 데이터 포인트 중 다수에 맞추려함(일반화)

*** 선형모델 - 회귀에서는 alpha값 커지면 규제 증가(모델 복잡도 감소) -> C와 반대

 

from sklearn.datasets import load_breast_cancer

cancer = load_breast_cancer()

X_train, X_test, y_train, y_test = train_test_split(

    cancer.data, cancer.target, stratify=cancer.target, random_state=42)

logreg = LogisticRegression(max_iter=5000).fit(X_train, y_train)

print("훈련 세트 점수: {:.3f}".format(logreg.score(X_train, y_train)))

print("테스트 세트 점수: {:.3f}".format(logreg.score(X_test, y_test)))

->훈련 세트 점수: 0.958 / 테스트 세트 점수: 0.958

-> 유방암 데이터셋 사용 load_breast_cancer / 기본값 C=1
-> 훈련, 테스트 세트 성능 0.95로 좋지만 서로 비슷 => 과소적합 추정                                                                                  

logreg100 = LogisticRegression(C=100, max_iter=5000).fit(X_train, y_train)

print("훈련 세트 점수: {:.3f}".format(logreg100.score(X_train, y_train)))

print("테스트 세트 점수: {:.3f}".format(logreg100.score(X_test, y_test)))

-> 훈련 세트 점수: 0.981 / 테스트 세트 점수: 0.965

-> C =100 => 훈련, 테스트 성능 둘다 조금 더 상승 -> C값 키우며 모델 복잡도 높임

 

logreg001 = LogisticRegression(C=0.01, max_iter=5000).fit(X_train, y_train)

print("훈련 세트 점수: {:.3f}".format(logreg001.score(X_train, y_train)))

print("테스트 세트 점수: {:.3f}".format(logreg001.score(X_test, y_test)))

-> 훈련 세트 점수: 0.953 / 테스트 세트 점수: 0.951

# C =0.01  => 기본매개변수 C =1보다 정확도 낮아짐
# 이미 과소적합된 모델에서 더 모델 복잡도 낮춤 -> 정확도 더 떨어짐

 

plt.plot(logreg100.coef_.T, '^', label="C=100")

plt.plot(logreg.coef_.T, 'o', label="C=1")

plt.plot(logreg001.coef_.T, 'v', label="C=0.001")

plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)

xlims = plt.xlim()

plt.hlines(0, xlims[0], xlims[1])

plt.xlim(xlims)

plt.ylim(-5, 5)

plt.xlabel("특성")

plt.ylabel("계수 크기")

plt.legend()

plt.show()

-> 매개변수 C에 따른 w계수값의 변화관찰
-> C값이 작을수록 W계수값 범위가 줄어듬(0에 가까워짐)

-> 로지스틱 회귀 logistic reg -> 기본적으로 릿지 사용(L2규제) -> w계수값 완전히 0되지 않음
-> 3번째 특성 'mean perimeter' -> C값이 작아졌지만 w계수값의 범위(절댓값)가 오히려 커짐 
-> w계수 클래스와 특성의 연관성 주의 -> 세번째 특성 'mean perimeter'은 양성이나 악성 신호 모두 될수 있음 - 두 클래스 둘 다 연관성 가질 수 있음 (다른 샘플은 악성샘플만 연관성있음 - 한 클래스 가짐)

-> 선형모델 계수는 항상 의심하고 조심해서 해석하기 (특정 특성이 두 클래스 모두와 관련있을 수 있으므로)

 

for C, marker in zip([0.001, 1, 100], ['o', '^', 'v']):

    lr_l1 = LogisticRegression(solver='liblinear', C=C, penalty="l1", max_iter=1000).fit(X_train, y_train)

    print("C={:.3f} 인 l1 로지스틱 회귀의 훈련 정확도: {:.2f}".format(

          C, lr_l1.score(X_train, y_train)))

    print("C={:.3f} 인 l1 로지스틱 회귀의 테스트 정확도: {:.2f}".format(

          C, lr_l1.score(X_test, y_test)))

    plt.plot(lr_l1.coef_.T, marker, label="C={:.3f}".format(C))

plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)

xlims = plt.xlim()

plt.hlines(0, xlims[0], xlims[1])

plt.xlim(xlims)

plt.xlabel("특성")

plt.ylabel("계수 크기")

plt.ylim(-5, 5)

plt.legend(loc=3)

plt.show()

-> C=0.001 인 l1 로지스틱 회귀의 훈련 정확도: 0.91
C=0.001 인 l1 로지스틱 회귀의 테스트 정확도: 0.92
C=1.000 인 l1 로지스틱 회귀의 훈련 정확도: 0.96
C=1.000 인 l1 로지스틱 회귀의 테스트 정확도: 0.96
C=100.000 인 l1 로지스틱 회귀의 훈련 정확도: 0.99
C=100.000 인 l1 로지스틱 회귀의 테스트 정확도: 0.98

 

-> 라쏘(L1규제)사용 -> w계수 0값 가능 -> 일부특성만 이용 가능 
-> LinearSVC (서포트 벡터 머신) -> loss 매개변수-> 손실함수 지정가능(기본값 : squred_hinge -> 제곱힌지손실)

*** 힌지손실hinge loss 이란?

-> 분류모델에서 주로 사용되는 손실함수loss function / 특히 서포트 벡터 머신 SVM에서 사용 

-> 힌지손실 hinge : penalty매개변수에 L2(릿지)만 가능

-> 제곱힌지손실 squared_hinge : 힌지손실에 이상치에 더 많은 패널티 부과 / penalty매개변수에 L1(라쏘) / L2(릿지) 둘다 가능

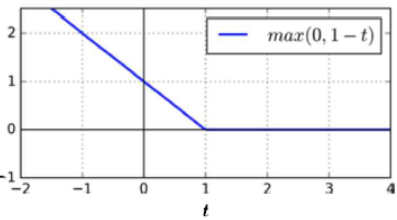
힌지 hinge = 경첩 ( 함수가 경첩 구조를 닮음)

서포트 벡터 머신 SVM의 목적 -> 데이터를 잘 구분하는 마진margin 을 최대한 크게 하기 

힌지 손실의 목적->  마진 바깥 관측값은 손실을 무시(loss = 0) / 마진 내 관측값 손실 크게 함 

 

*** 주의) LogisticRegression -> penalty매개변수에 L1/L2/elasticnet/None(규제 없음)가능 / 이외에도 다양한 매개변수값 변경이 가능함(solver = 'saga' / 'liblinear' 등등)  

 

***경첩그림

*** 힌지 손실 함수 hinge loss function

*** 서포트 벡터 머신 SVM의 마진margin

 

# 다중분류 Multiclass Classification (클래스 3이상으로 분류)

선형분류모델은 대부분 이진분류 지원함 (로지스틱 회귀 제외) 

즉, 선형분류모델은 대부분은 다중분류 지원하지 않는다 

 

그렇다면 다중분류는 어떻게 수행해야할까?

이진분류를 다중분류로 확장하는 기법 : 일대다 방법 ( one vs rest 혹은 one vs all)

-> 클래스 수만큼 이진분류 모델 만듦 예) 3개 분류 -> 이진분류r 3

-> 각 클래스마다 w계수,b절편 가짐 

-> 모든 이진 분류기 중 함수의 가장 높은 값을 내는 분류기 클래스를 예측 값으로 선택

from sklearn.datasets import make_blobs

X, y = make_blobs(random_state=42)

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)

plt.xlabel("특성 0")

plt.ylabel("특성 1")

plt.legend(["클래스 0", "클래스 1", "클래스 2"])

plt.show()

-> 세 클래스 가진 2차원 데이터에 Linear SVC(Linear Support Vector Classifier) 훈련

linear_svm = LinearSVC().fit(X, y)

print("계수 배열의 크기: ", linear_svm.coef_.shape)

print("절편 배열의 크기: ", linear_svm.intercept_.shape)

-> 계수 배열의 크기:  (3, 2) / 절편 배열의 크기:  (3,) -> 세클래스로 분류하므로 계수, 절편 3개 

-> coef_ 행 -> 세 클래스 대응하는 w계수벡터 / 열 -> 각 특성에 따른 w계수값(이 데이터셋에서는 2개 가짐)
-> intercept_ ->  각 클래스 절편 (1차원 벡터)

 

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)

line = np.linspace(-15, 15)

for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,

                                  mglearn.cm3.colors):

    plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)

plt.ylim(-10, 15)

plt.xlim(-10, 8)

plt.xlabel("특성 0")

plt.ylabel("특성 1")

plt.legend(['클래스 0', '클래스 1', '클래스 2', '클래스 0 경계', '클스 1 경계',

            '클래스 2 경계'], loc=(1.01, 0.3))

plt.show()

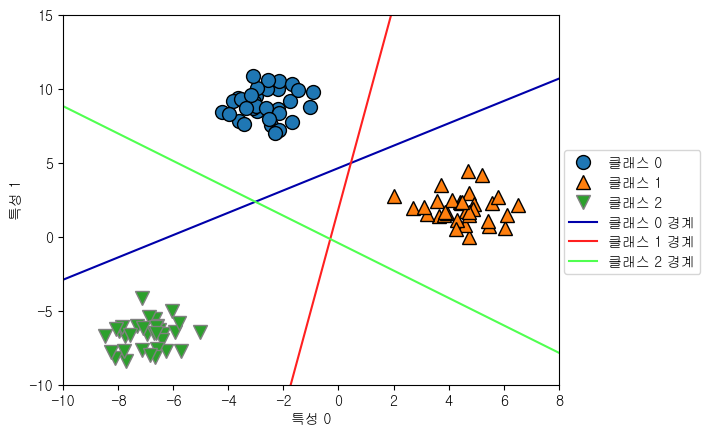
-> 세 이진 분류기가 만드는 경계 시각화

 

mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)

mglearn.discrete_scatter(X[:, 0], X[:, 1], y)

line = np.linspace(-15, 15)

for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,

                                  mglearn.cm3.colors):

    plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)

plt.legend(['클래스 0', '클래스 1', '클래스 2', '클래스 0 경계', '클래스 1 경계',

            '클래스 2 경계'], loc=(1.01, 0.3))

plt.xlabel("특성 0")

plt.ylabel("특성 1")

plt.show()

-> 다중 클래스 분류기의 결정경계표현
-> 분류공식 결과가 가장 높은 클래스로 분류함(가장 가까운 직선의 클래스로 분류)

 

# 선형모델 linear model 정리

<선형모델 주요 매개변수>
-> 회귀 모델 => alpha -> alpha값 클수록(규제 강하게) 모델 단순

-> 분류 모델 - LinearSVC, LogisticRegression => C ->  C값 작을수록(규제 약하게) 모델 단순

-> alpha, C -> 로그 스케일로 최적치 결정 (보통 0.01 /0.1 /1/ 10 -> 10배씩 적용)

-> 이후  L1(릿지) / L2(라쏘) 규제 사용할지 정함

-> 중요특성 많다 -> L2 / 적다 -> L1

 

<선형모델 장점>

-> 학습, 예측빠름 / 큰데이터셋, 희소데이터 셋 잘 작동 / 어떻게 예측 만들어지는지 쉽게 이해 가능 / 샘플에 비해 특성 많을 때 잘 작동함 (고차원 모델)

but 저차원 -> 다른 모델이 일반화 성능 더 좋음 

 

<대용량 데이터 빠르게 처리방법>
-> LogisticRegression, Ridge에 solver='sag' 옵션 지정
*** sag

-> Stochastic Average Gradient descent(확률적 평균 경사 하강법)

-> 반복 진행할 때 이전 모든 경사 평균 사용하여 계수 갱신함 

혹은

-> 선형모델 SGDClassifier / SGDRegressor 사용

 

# 번외) 메서드 연결 method chaining

 

 

logreg = LogisticRegression(max_iter=5000)

y_pred = logreg.fit(X_train, y_train).predict(X_test)

-> 모델 객체생성 / 훈련, 예측 한줄입력

y_pred = LogisticRegression(max_iter=5000).fit(X_train, y_train).predict(X_test)

-> 코드 짧게 작성 바람직하지 않음 -> 코드 읽기(해석하기) 어려워짐
-> 학습된 모델 변수에 남지 않음(예측 결과만 담은 변수만 남음) -> 새 데이터 예측 불가능