Hippo's data
[Paper review] TimesNet 본문
오늘날까지도 TSF(Time-series Forecasting)에서 압도적인 성능을 보여주고 있는 TimesNet에 대해 알아보도록 하겠습니다!
특히 시계열 데이터를 1D Vision Task로 치환해서 시계열 예측에 도입했던 TCN 모델과 유사하게 TimesNet는 2D Vision Task로 치환해서 시계열 예측에 도입한 모델입니다!
간단한 논문리뷰와 예제 데이터를 통한 실습까지 진행해보도록 하겠습니다!
Paper: TIMESNET: TEMPORAL 2D-VARIATION MODELING FOR GENERAL TIME SERIES ANALYSIS
(Haixu Wu, Tengge Hu, Yongliu Liu, Hang Zhou, Jianmin Wang, Mingsheng Long)
- Conference: ICLR 2023
- GitHub Repository: https://github.com/thuml/Time-Series-Library
- ArXiv: https://arxiv.org/abs/2210.02186
GitHub - thuml/Time-Series-Library: A Library for Advanced Deep Time Series Models for General Time Series Analysis.
A Library for Advanced Deep Time Series Models for General Time Series Analysis. - thuml/Time-Series-Library
github.com
TimesNet: Temporal 2D-Variation Modeling for General Time Series Analysis
Time series analysis is of immense importance in extensive applications, such as weather forecasting, anomaly detection, and action recognition. This paper focuses on temporal variation modeling, which is the common key problem of extensive analysis tasks.
arxiv.org
다양한 주기(period) 포착→ 시계열 분석을 2D vision task로 치환
1. SUMMARIZE
| 항목 | 핵심 내용 |
| Problem | 1D 시계열 표현 한계, 다중 주기성(Multi-periodicity) -> 현실의 시계열 데이터는 여러 주기가 중첩된 복잡한 형태 -> 기존 1D 모델(RNN, TCN, Transformer)은 인접 시점의 정보만 포착할 뿐, 서로 다른 주기 간의 변동성(Temporal Variation)을 효과적으로 모델링하지 못함 |
| Method | 1. 1D to 2D Transformation (구조 변환) • Periodicity Discovery: FFT(고속 푸리에 변환)를 수행하여 데이터 내에서 Top-k개의 주기(Period) 감지 • Reshape: 감지된 주기를 기준으로 1D 시계열을 2D 텐서로 변환 → '주기 내 변동(Intra-period, 열)', '주기 간 변동(Inter-period, 행)'을 2D로 구조화 2. TimesBlock (특징 학습) • 2D Vision Backbone: 변환된 2D 텐서에 Inception Block을 적용하여, 다양한 크기의 커널(Multi-scale)로 2D 공간의 지역적/전역적 패턴을 동시에 학습 • Adaptive Aggregation: 각 주기별로 학습된 k개의 표현(Representation)을 주파수 진폭(Amplitude) 기반 가중합으로 결합하여 최종 출력 생성 |
| Results | 범용적인(Task-General) 시계열 분석 성능 입증 장/단기 예측, 결측치 보간, 분류, 이상 탐지 등 5가지 주요 시계열 태스크에서 SOTA |
| Contribution | Time Series Analysis as 2D Computer Vision 시계열 데이터를 1D 시퀀스가 아닌 2D 비전 문제로 치환하는 새로운 프레임워크를 제안 복잡한 시계열 전용 모듈 설계 없이도, 검증된 최신 2D 비전 백본 모델(ResNet, Swin Transformer 등)을 시계열 분석에 직접 적용할 수 있는 범용적인 기반(Foundation)을 마련 |
2. DETAIL
1. Introduction

기존 1D 구조 한계: 인접한 시점간 변동만 파악
→ intraperiod, interperiod 활용하여 1D → 2D 로 재구성
- intraperiod(= 주기 내 변동):
- 특정 주기 안에서의 변화 패턴
- 열(columns)
- 예) 1월의 30일 변화 패턴
- interperiod(= 주기 간 변동):
- 서로 다른 주기 간 변화 패턴
- 행(rows)
- 예) 1,2,3 … 각 월 끼리의 변화 패턴
2. RELATED WORK
기존 방법론
- 정의된 패턴 가정한 모델 - ARIMA, Holt-Winter, Prophet
- 실제 현실에서는 복잡한 변동성으로 인해 정의된 패턴으로 커버 불가능
- 딥러닝 기반
- RNN 기반 - 장기의존성 한계, 계산 비효율성
- TCN 기반 - 지역적 특성 포착에는 장점 / 장기 의존성 한계
- Transformer 기반 - 시점간 쌍별(pair-wise) 의존성 포착 / 명확한 의존성 포착 한계
기존 1D 시계열 한계
- 인접 시점 정보 포착은 잘하지만, 여러 시점에 걸친 패턴 포착에는 한계점 존재
→ 2D 시계열 제안
3. TIMESNET
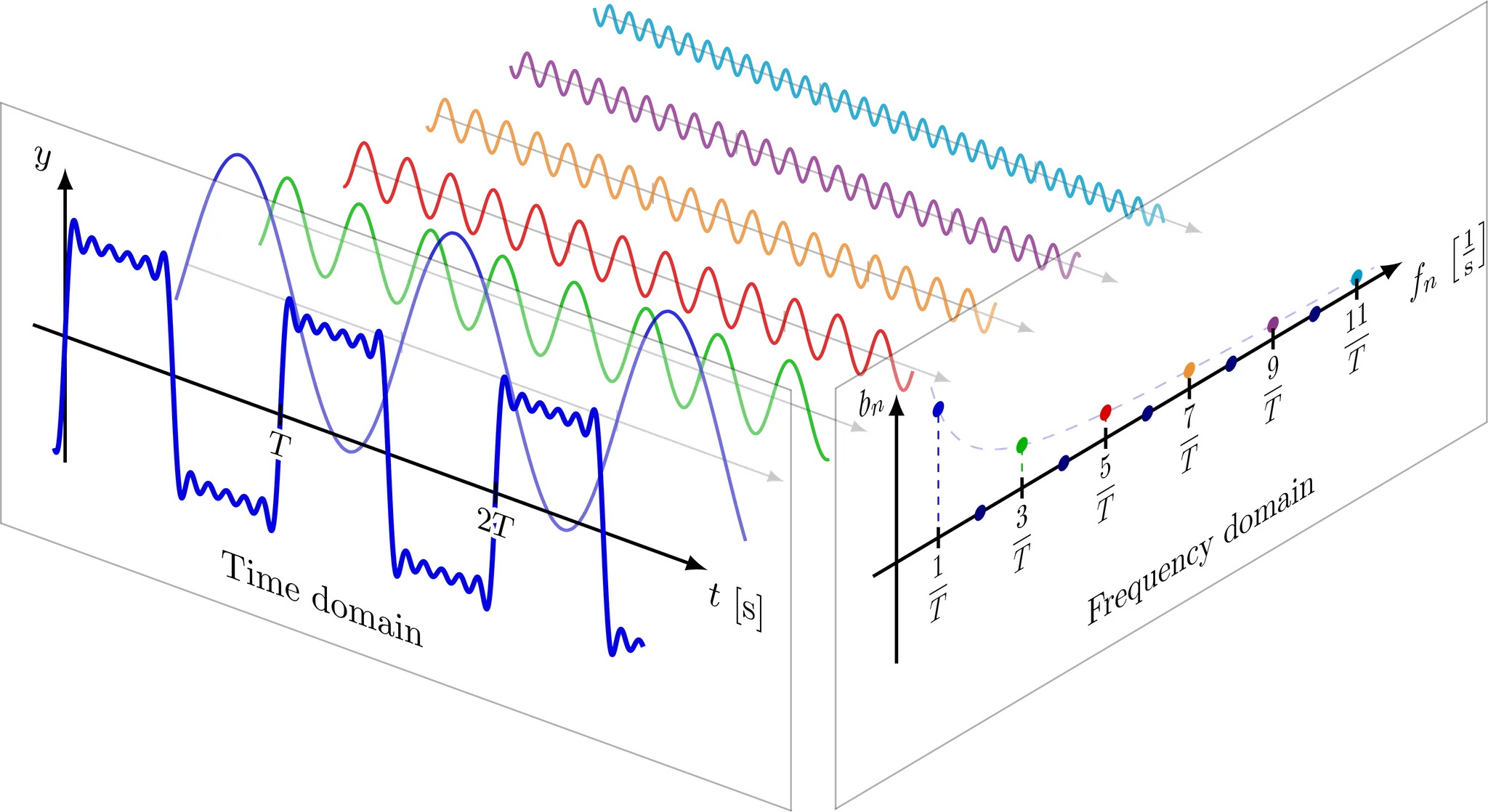
3.1 TRANSFORM 1D-VARIATIONS INTO 2D-VARIATIONS
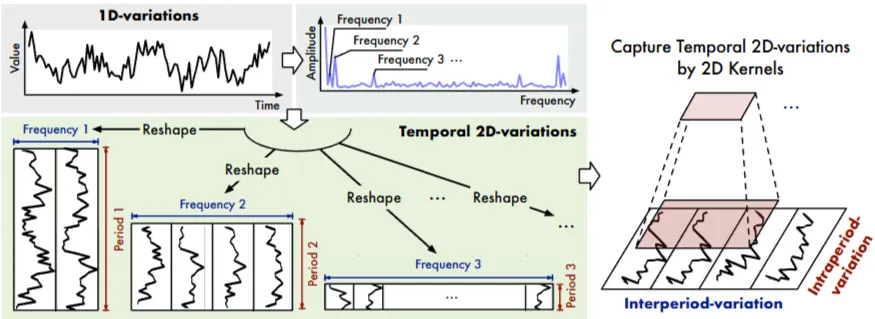
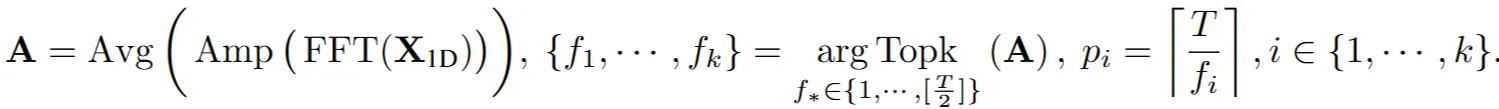
→ FFT 적용하여 Top k개의 주파수를 찾아내어 각각 k개의 주기 길이를 계산
- $X_{1D}∈R^{T×C}$: 1차원 시계열 데이터
- $FFT(X_{1D})$: 1차원 시계열 데이터에 FFT(Fast Fourier Transform, 고속 푸리에 변환) 적용
- $Amp(⋅)$: 분해된 각 주파수 스펙트럼 진폭(amplitude, 높이) 계산
- Avg(⋅): 여러 변수(multivariate)의 진폭 평균 (단변량(univariate)일 경우, 생략)
즉, A는 각 주파수들의 상대적인 중요도 나타냄
- $f_1,…,f_k$: A에서 가장 큰 k개(hyper-parameter)의 진폭 값을 갖는 주파수들 선택
- 목적
- 주파수 도메인 희소성(Sparsity) 고려 - 특정 주파수에 주기성이 몰려있는 특징 고려
- 고주파 노이즈 제외
- 목적
- $Topk_{f∗∈{1,…,⌊T/2⌋}(A)}$: 해당 선택된 주파수 인덱스 탐색
- 1 ~ $⌊T/2⌋$: 1부터 총 시계열 길이 T의 절반까지 탐색(FFT를 통해 분해된 주파수는 대칭성을 가지기 때문→ 주파수 영역의 켤레성 (conjugacy of frequency domain))
- $pi=⌈T/fi⌉$: 각 선택된 주파수 $f_i$ 에 해당하는 주기(period) $p_i$ 계산
- 주기계산 → 시계열 길이 T를 해당 주파수 $f_i$로 나눔 (올림연산 → 정수값)
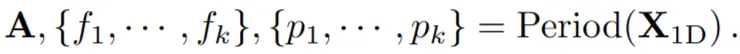
→ 위의 과정을 요약한(summarize) 수식
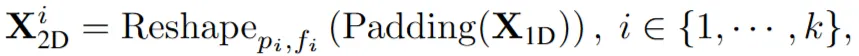
1D → 2D 변환
- $Padding(X_{1D})$: 2D 텐서 형태로 구성하기 위해 제로 패딩 추가
- $Reshape_{p_i, f_i}$: 1D → 2D ( $p_i$개 행과 $f_i$개 열)
- $p_i$: 행, 주기 길이, interperiod = adjacent periods
- $f_i$: 열, 해당 주기에 대한 주파수(frequency)의 역수, intraperiod = adjacent time points
- 주기(p): 한 번 반복되는 데 걸리는 시간
- 주파수(f): 단위 시간당 반복되는 횟수
- f=1/p (역수관계)
| 💡푸리에 변환( Fourier Transform)이란? → 복잡한 신호는 단순한 파동들의 합으로 표현 가능함 정의: 시간에 따라 변하는 신호(Time Domain) → 주파수 성분(Frequency Domain)으로 분해 |
| 구분 | DFT (Discrete Fourier Transform) | FFT (Fast Fourier Transform) |
| 정의 | 이산 데이터를 주파수로 변환하는 수학적 공식(Definition) | DFT를 컴퓨터가 빠르게 계산하기 위한 고속 알고리즘(Implementation) |
| 방식 | 데이터 전체를 1:1로 내적하여 계산 | 데이터를 반으로 쪼개는 분할 정복(Divide & Conquer) 방식 |
| 속도 | O(N^2) (느림) | O(N log N) (매우 빠름) |
3.2 TIMESBLOCK
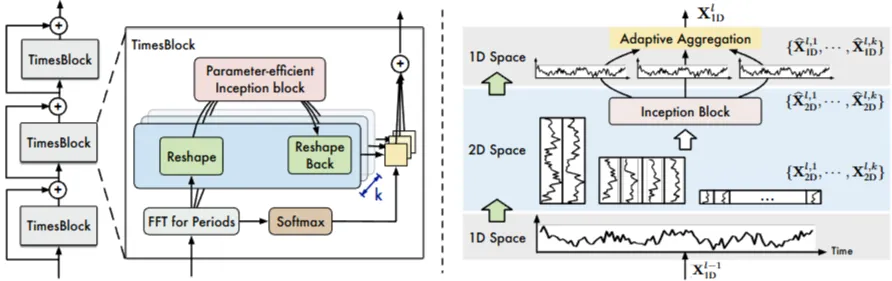
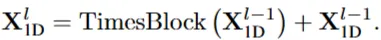
→ 각 레이어 l의 연산
→ 잔차 연결(residual connection) 구조: TimesBlock 출력을 이전 레이어의 출력에 더하여 다음 레이어의 출력 생성
Capturing temporal 2D-variations

주기추출, 2D 텐서로 변환, Inception블록을 이용하여 특징추출, 1D로 변환
- Trunc(⋅): 패딩으로 인해 추가된 부분 제거, 기존 시계열 길이 T에 맞게 자름
- Shared Inception Block
- 시계열에서 발견된 'K'개의 주기성 각각에 대해 생성된 2D 텐서들을 처리하기 위해 동일한 하나의 Inception block 공유(shared)
- 추출된 주기성 수 K에 관계없이 모델의 전체 크기는 크게 변하지 않음(model size invariance)
Adaptive aggregation

→ 여러 주기에 대해 처리된 2D 텐서 특징($X_{ID}^{l,i}$)들을 중요도 가중치($A_{f_i}^{l−1}$)와 곱하여 결합
- $A_{f_i}^{l−1}$: 각 주파수의 진폭(amplitude = 중요도 가중치)을 Softmax 함수를 이용하여 확률로 표현(0~1, 총합=1)
Generality in 2D vision backbones
다양한 2D 백본(Inception, ResNet, Swin Transformer, ConvNeXt 등)을 시계열 분석에 활용가능
4. EXPERIMENTS

Baselines
- RNN 기반: LSTM (1997), LSTNet (2018), LSSL (2022)
- CNN 기반: TCN (2019)
- MLP 기반: LightTS (2022), DLinear (2023)
- Transformer 기반: Reformer (2020), Informer (2021), Pyraformer (2021a), Autoformer (2021), FEDformer (2022), Non-stationary Transformer (2022a), ETSformer (2022)
- 각 작업별 최신 모델: 단기 예측을 위한 N-HiTS (2022) 및 N-BEATS (2019), 이상 탐지를 위한 Anomaly Transformer (2021), 분류를 위한 Rocket (2020) 및 Flowformer (2022)
4.1 MAIN RESULTS
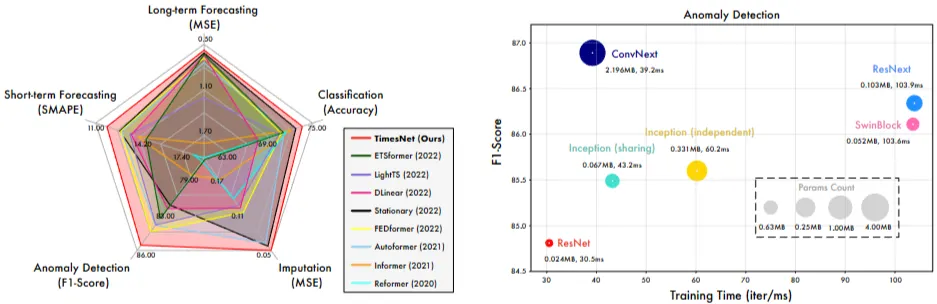
- (좌) 장기 예측, 단기 예측, 결측치 보간, 분류, 이상 탐지 등 다섯 가지 분야에서 SOTA 달성
- (우) 다양한 비전 백본 모델로 교체 → 더 효과적인 성능 확보 가능
4.2 SHORT- AND LONG-TERM FORECASTING
Long-term Fcst
- past sequence length, Fcst length
- ILI Dataset: 36, {24, 36, 48, 60}
- Others: 96, {96, 192, 336, 720}

Short-term Fcst
- Fcst length: [6, 48]

→ Long-term, Short-term FCST에서 대부분 SOTA 달성
4.3 IMPUTATION
randomly mask {12.5%, 25%, 37.5%, 50%}
96 length

→ SOTA 달성
4.4 CLASSIFICATION

- UEA Time Series Classification Archve 데이터셋 - multivariate(10개 변수)
- 기존 SOTA Rocket, Deep model Flowformer 뛰어넘는 성능
4.5 ANOMALY DETECTION
- 5가지 이상탐지 벤치마크 데이터셋
- SMD, MSL, SMAP, SWaT, PSM
- sliding window 방식 → 연속적, 겹치지않는 segment로 분할

- FEDformer, Autoformer 같은 advanced Transformer기반 모델 능가
- 일반적인Transformer기반 모델은 평균적으로 낮은 점수
- 다수의 정상시점에 의해 오판될 가능성 존재 (이상탐지는 희귀한 비정상 패턴을 식별해야 하는 반면)
- 주기성 추출한는 모델(TimesNet, FEDformer, Autoformer) 우수한 성능 → 이상탐지에 주기성 고려 중요
4.6 MODEL ANALYSIS
Representation analysis
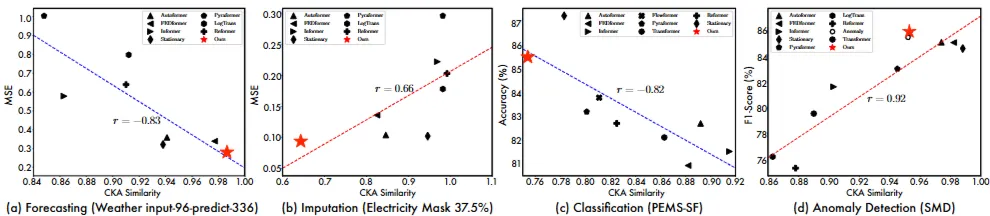
CKA similarity (Centered Kernel Alignment)
- 신경망의 다른 계층(layer)에서 학습한 표현(representation) 간의 유사성 측정
- 높음: 계층간 표현이 유사 → 신경망이 깊어지더라도 학습되는 특징들이 크게 변하지 않음 (저low 수준의 일반적인 특징 학습)
- 낮음: 계층별 표현이 구별됨 → 신경망이 깊어지면서 특징들이 다른 방식으로 학습, 계층적(hierarchical) 학습 접근 방식(계층별로 다른 표현 학습 - 일반적인 특징, 복잡한 특징 등)
- 각 Task 별로 적합한 표현능력(Representation) 존재 → 각 Task별 성능과 CKA similarity 상관관계 높음
- 보간(Imputation), 이상 탐지(Anomaly Detection) → 높은 CKA 유사도 효과적 (일반적인 저수준low 패턴 학습이 중요함)
- 예측(Forecasting), 분류(Classification) → 낮은 CKA 유사도 효과적 (복잡한 패턴, 계층적 표현 학습 중요)
→ TimesNet은 각 작업에 적합한 표현을 학습 → 범용적으로 활용 가능
→ FEDformer는 예측, 이상 탐지 작업에서 우수한 성능 / 보간, 분류에는 계층적 표현 학습 어려움
Temporal 2D-variations

→ 원본 1D 시계열 데이터를 여러 주기를 기준으로 변환한 2D 텐서
→ 특정 주파수(Frequency)와 해당 주파수에 따른 주기(Period) 길이
- 행(Rows): 기간 간 변동(Interperiod-variation)
- 열(Columns): 기간 내 변동(Intraperiod-variation)
→ 특정 시점이나 주기에서 나타나는 강한 변동성 확인
3. Implementation
https://github.com/thuml/Time-Series-Library
GitHub - thuml/Time-Series-Library: A Library for Advanced Deep Time Series Models for General Time Series Analysis.
A Library for Advanced Deep Time Series Models for General Time Series Analysis. - thuml/Time-Series-Library
github.com
- Dataset: Airline Passengers
https://raw.githubusercontent.com/jbrownlee/Datasets/master/airline-passengers.csv
- 총 길이: 144개월 (12년), 월별 기록
- 모델 아키텍처 - 비전 백본으로 inception v1 사용
| Model( (model): ModuleList( (0-1): 2 x TimesBlock( (conv): Sequential( (0): Inception_Block_V1( (kernels): ModuleList( (0): Conv2d(16, 32, kernel_size=(1, 1), stride=(1, 1)) (1): Conv2d(16, 32, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (2): Conv2d(16, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (3): Conv2d(16, 32, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3)) (4): Conv2d(16, 32, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4)) (5): Conv2d(16, 32, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5)) ) (1): GELU(approximate='none') (2): Inception_Block_V1( (kernels): ModuleList( (0): Conv2d(32, 16, kernel_size=(1, 1), stride=(1, 1)) (1): Conv2d(32, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)) (2): Conv2d(32, 16, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)) (3): Conv2d(32, 16, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3)) (4): Conv2d(32, 16, kernel_size=(9, 9), stride=(1, 1), padding=(4, 4)) (5): Conv2d(32, 16, kernel_size=(11, 11), stride=(1, 1), padding=(5, 5)) ) (enc_embedding): Linear(in_features=1, out_features=16, bias=True) (layer_norm): LayerNorm((16,), eps=1e-05, elementwise_affine=True) (predict_linear): Linear(in_features=96, out_features=120, bias=True) (projection): Linear(in_features=16, out_features=1, bias=True) ) |
- 파라미터
| class Configs: seq_len = 96 # 입력 길이 pred_len = 24 # 예측 길 enc_in = 1; c_out = 1 d_model = 16; d_ff = 32 e_layers = 2 num_kernels = 6 top_k = 3 # 3개의 주기 사용 learning_rate = 0.001 batch_size = 64 epochs = 200 |
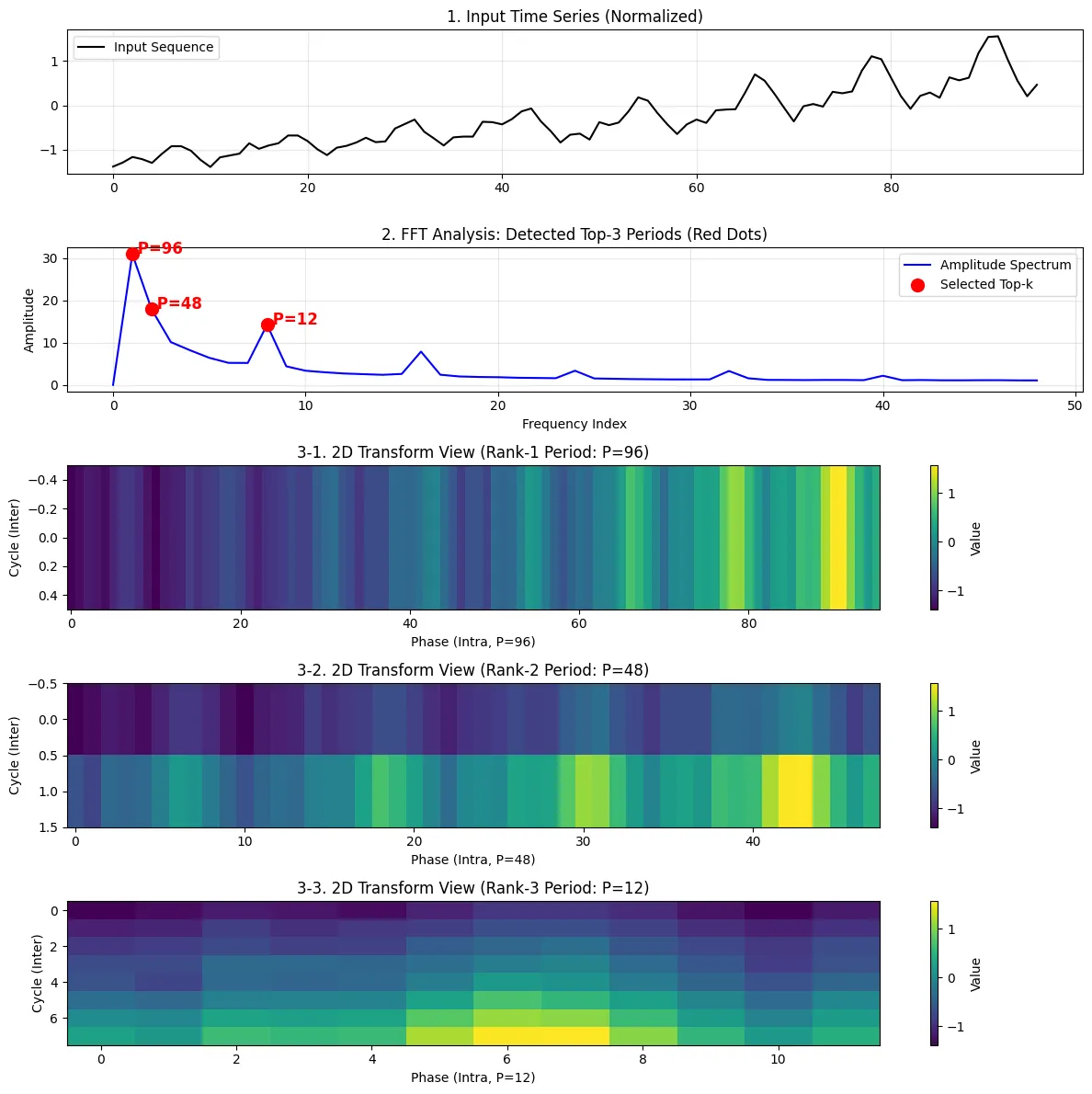
- 각 변환된 2D 텐서 시각화
- top 3개 주기
- 96, 48, 12 주기로 추출됨
- 96 = 1 X 96 → 전체 주기 : Trend
- 48 = 2 X 48
- 12 = 8 X 12 → 1년(12월) 주기
- 가로축 (Width = 12): 1월, 2월, ..., 12월 (계절 안에서의 변화, Intra-period)
- 여름 휴가철(6,7월) 진한 노란색
- 세로축 (Height = 8): 1년차, 2년차, ..., 8년차 (연도 간의 변화, Inter-period)
- 가로축 (Width = 12): 1월, 2월, ..., 12월 (계절 안에서의 변화, Intra-period)
- 96, 48, 12 주기로 추출됨
- top 3개 주기

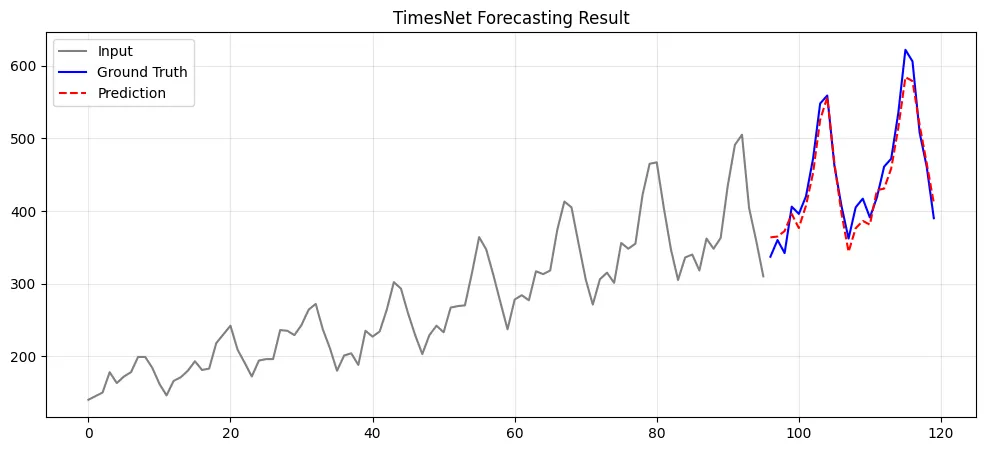
- 예측 결과 시각화
- FFT 변환
- top 3개 주기로 원본 데이터셋 분해
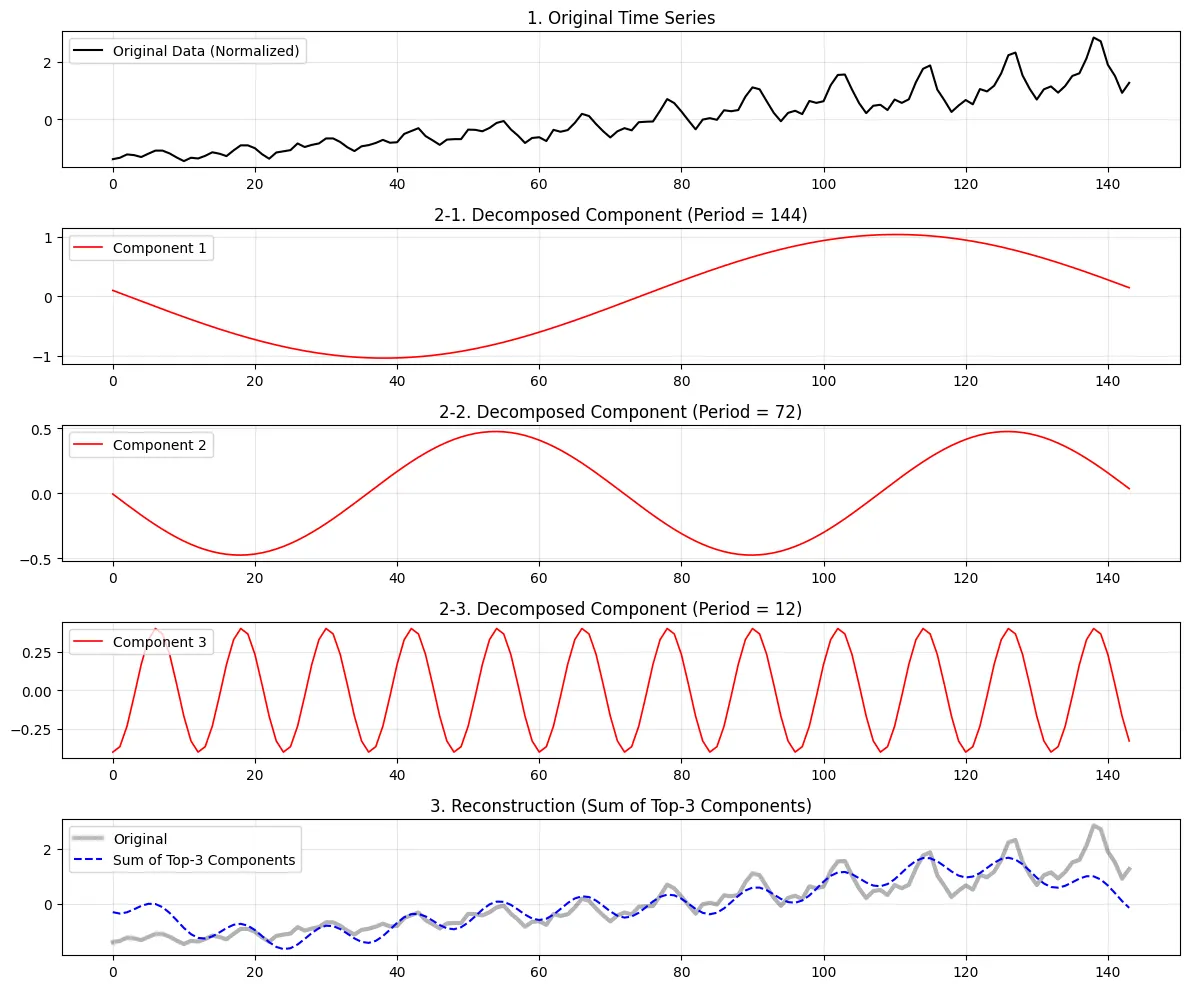
- 학습 과정
[입력 데이터 (1D 시계열)]
│
├───> (복사 1) ──[Reshape: 96마다]──> [2D 텐서 A: 1 x 144] ──[Conv2D]──> 특징 A 추출
│
├───> (복사 2) ──[Reshape: 48마다]───> [2D 텐서 B: 2 x 72 ] ──[Conv2D]──> 특징 B 추출
│
└───> (복사 3) ──[Reshape: 12마다]───> [2D 텐서 C: 12 x 12] ──[Conv2D]──> 특징 C 추출
│
┌─────────────────────────────────────────────────────────────────────────┘
│
▼
[결과 합산 (Weighted Sum)] -> 다시 1D로 펴서 합침
4. Questions
- 비주기적(Non-periodic) 데이터 효과적인지?
- TimesNet은 데이터에서 주기성을 추출하여 학습하는 모델 → 주기성이 전혀 없는 데이터셋의 경우에는 어떤 결과
- 패딩(Padding) 전략 비교(현재는 제로패딩)
- 다른 방식의 패딩(예: 복제 패딩, 평균값 패딩 등)을 사용 후, 결과 차이
- 다양한 비전백본 모델(현재는 inception v1 이용중) 확장
- ConvNeXt, ResNet, Swin Transformer 등 다양한 모델 사용 후, 결과 차이
'Paper review' 카테고리의 다른 글
| [Paper review] Pre-LN(Pre-Layer Normalization) (0) | 2026.02.09 |
|---|---|
| [Paper review] iTransformer (1) | 2026.02.04 |
| [Paper review] PatchTST (0) | 2026.01.30 |
| [Paper review] GAN(Generative Adversarial Nets) (0) | 2026.01.29 |
| [Paper review] DLinear (0) | 2026.01.12 |




