쉘 정렬(Shell Sort)

오늘은 정렬 알고리즘인 쉘 정렬(Shell Sort)에 대해 알아보겠습니다!

쉘 정렬(Shell Sort)의 쉘(Shell)은 1959년 해당 알고리즘을 고안한 도널드 셸(Donald L. Shell)의 이름을 따서 지어졌는데욥

삽입 정렬(Insertion Sort)의 개선된 버전으로 값을 비교하며 정렬하는 비교정렬에 속합니다!

https://hipposdata.tistory.com/108

삽입 정렬 (Insertion Sort) 알고리즘

 

# 동작과정 

데이터를 일정 간격(gap)으로 나누어 부분 배열을 정렬한 뒤, 점차 간격(gap)을 줄여가며 정렬하는 알고리즘입니다!

특히 일정 간격(gap)으로 나뉜 부분배열 정렬시 삽입 정렬(Insertion Sort)을 이용하는데요

데이터가 간격을 줄이며 정렬해가며 점점  정렬된 상태가 되므로 

어느정도 정렬된 상태에서 빠르게 작동하는 삽입 정렬(Insertion Sort)의 장점을 극대화할 수 있습니다!

 

일정 간격(gap)은 보통 초기에 데이터 절반크기로 설정하며,  gap = n/2

이후 간격(gap)의 크기를 절반씩 줄이고, gap = gap/2 

간격(gap)이 gap = 1 일시 최종정렬 후 종료하게 됩니다

 

특히 간격(gap)은 짝수이면 1을 더하여 홀수로 만들어 줍니다!

간격(gap)이 홀수라면, 짝수, 홀수 인덱스가 겹처서 비교가 이루어지므로 전체 데이터가 정렬되지만,

간격(gap)이 짝수라면, 균등하게 분할되므로 짝수, 홀수번째 인덱스끼리만 각각 정렬되며 서로 섞이지 않게된다

 

예)  [8, 3, 7, 2] 오름차순 정렬
gap = 2

짝수 인덱스 0,2끼리 정렬
홀수 인덱스 1,3끼리 정렬
-> 7, 2, 8, 3
-> 전체 값은 정렬되지 않음 

 

쉘 정렬은 부분배열로 나누어 정렬이 진행되므로 넓은 의미에서 분할 정복(Divide and Conquer) 방식으로도 불리는데요

하지만, 쉘 정렬에서는 순환 호출(recursive call)이 일어나지 않으므로 좁은 의미에서는 분할정복이 아니라고 바라보기도 합니다 

 

예시를 통해 구체적인 동작과정을 알아보겠습니다!

9,8,3,7,5,6,4,1 총 8개의 데이터를 오름차순으로 정렬해보겠습니다

 

# Python 코드

쉘정렬을 파이썬으로 구현해 보았습니다!

쉘정렬에서 삽입 정렬(Insertion Sort)이 사용되는데요

기존 삽입정렬은 1씩 빼가며 비교했다면 

쉡 정렬의 삽입정렬은 gap 만큼 빼가며 삽입할 위치를 찾습니다!

# 쉘 정렬 알고리즘

def shell_sort(A):

    n = len(A)

    gap = n // 2  # 초기 간격: 리스트 크기의 절반

    while gap > 0:  # 간격이 0보다 클 때까지 반복

        if gap % 2 == 0:  # gap이 짝수라면 1을 더해서 홀수로 만든다

            gap += 1

        for i in range(gap):  # 각 부분 리스트에 대해 삽입 정렬 수행

            sort_gap_insertion(A, i, n - 1, gap) # 부분리스트, 시작, 끝, 간격

        print('Gap:', gap, A)  # 중간 결과 출력

        gap = gap // 2  # 간격을 절반으로 줄임

# 부분 리스트 삽입 정렬

def sort_gap_insertion(A, first, last, gap):

    for i in range(first + gap, last + 1, gap):  # gap 간격으로 요소를 순회

        key = A[i]  # 삽입할 요소

        j = i - gap

        while j >= first and A[j] > key:  # 삽입 위치 찾기

            A[j + gap] = A[j]  # 요소 이동

            j = j - gap

        A[j + gap] = key  # 최종 위치에 삽입

# 테스트

data = [9, 8, 3, 7, 5, 6, 4, 1]  # 예제 데이터

shell_sort(data)

print("최종 정렬 결과:", data)

 

Gap: 5 [6, 4, 1, 7, 5, 9, 8, 3]
Gap: 3 [6, 3, 1, 7, 4, 9, 8, 5]
Gap: 1 [1, 3, 4, 5, 6, 7, 8, 9]
최종 정렬 결과: [1, 3, 4, 5, 6, 7, 8, 9]

 

# 성능분석 - 시간복잡도

 

최악(Worst)의 경우, 삽입정렬의 최악의 경우와 동일하게 O(n^2)의 시간복잡도를 보입니다

평균(Average)적인 경우, O(n √n) = O(n^1.5)의 시간복잡도를 보입니다

 

특히 비교정렬 중 빠른 성능을 보이는 O(nlogn) 의 정렬보다는 느리게 정렬되겠네욥,,,

증가폭) O(nlogn) < O(n^1.5) 

-> O(nlogn) 이 더 효율적

 

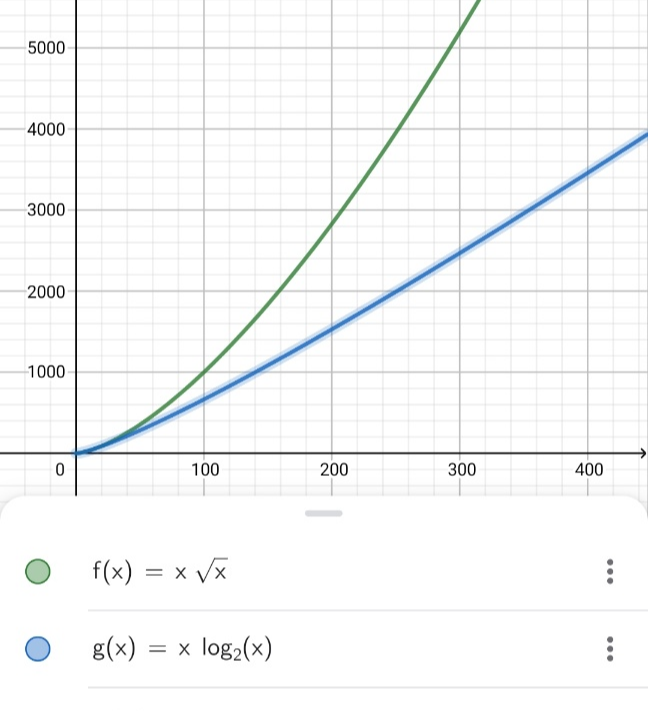
O(n) < O(nlogn) < O(n^1.5) <  O(n^2) 

 

# reference

파이썬 자료구조와 알고리즘: for beginner. (2021). 대한민국: 한빛아카데미.