Hippo's data
Median of medians 알고리즘 - 선택문제(Selction Problem) 본문
Median of medians 알고리즘 - 선택문제(Selction Problem)
Hippo's data 2024. 11. 30. 03:39오늘은 선택문제(Selction Problem)에 속하는 Median of medians 알고리즘에 대해 알아보겠습니다!
지난번에 선택문제에 대해 다뤘었는데욥 다시 복습하자면
선택문제란, k번째로 작은(또는 큰) 요소를 찾는 문제입니다!
해당 문제를 해결하는 방법에는 여러 전략이 존재하는데욥
1) 매번 큰 값을 찾아 k번째 큰 값을 찾기
가장 쉽게 생각할 수 있는 전략이다
매번 큰 값을 찾아 총 k번 큰 값을 찾으면, k번째로 큰 값을 찾을 수 있다
총 비교횟수를 생각해보면
1st max : n-1
2nd max: (n-1) + (n-2) = 2n-3
3rd max: (n-1) + (n-2) + (n-3)
k번째 max: (n-1) + (n-2) + (n-3) + ... + (n−k)
등차수열의 합: 항의개수k x (첫항 + 끝항) / 2해당공식을 이용하면
(n-1) + (n-2) + (n-3) + ... + (n−k) = k(2n-k-1) / 2
평균적 O(kn)
k = n 일경우(매번 큰값을 찾을 때 제일 작은 값이 몇번째로 큰값인지 찾는 경우)
즉, 최악의 경우엔 O(n^2) 의 시간이 소요된다
2) 기존 비교정렬 방식을 통해 정렬을 진행한 후, k번째 요소를 선택하는 방법
해당 방법은 비교정렬의 시간복잡도에 따라 선택문제 해결 시간이 결정되는데욥
버블 정렬, 선택 정렬, 삽입 정렬과 같은 방식을 사용한다면, O(n²)으로 정렬을 진행한후, k번째 값을 선택하게 되고
병합 정렬, 퀵 정렬, 힙 정렬과 같은 방식 사용시 평균적으로 O(nlogn)로 정렬을 진행한후, k번째 값을 선택하게 됩니다
하지만 이러한 방식은 아무리 빨라도 비교정렬 시간 성능의 하한(lower bound)인 O(nlogn)의 시간복잡도로 선택문제가 해결됩니다!
https://hipposdata.tistory.com/105
비교정렬 시간 성능의 하한(lower bound): O(nlogn)
안녕하세욥! 오늘은 비교 기반의 정렬 알고리즘(Comparison-based Sorting) 시간 성능의 하한(lower bound)에 대해 알아보겠습니다!! 비교 기반의 정렬 알고리즘(Comparison-based Sorting)에는 여러 종류가 있는
hipposdata.tistory.com
3) 퀵 선택(Quick selct) 이용
퀵 선택(Quick selct) 은 지난 포스팅에서 소개헸었는데욥
퀵 정렬(Quick sort) 에서 피벗으로 분할된 한쪽 부분만 재귀적으로 정렬을 진행하면서 평균적으로 O(n)의 시간복잡도로 정렬을 진행할 수 있지만 최악의 경우 O(n^2)의 시간복잡도로 k번째 수가 선택됩니다
https://hipposdata.tistory.com/112
퀵 선택(Quick selct) 알고리즘
안녕하세욥 오늘은 선택 문제(Selection Problem) 의 해결방법 중 하나인 퀵 선택(Quick selct)에 대해 알아겠습니다! # 선택 문제(Selection Problem) 란? 선택 문제(Selection Problem)는 특정 순위의 요소를 찾는
hipposdata.tistory.com
최악의 경우에도 O(n) 선형시간(Linear-time)의 시간복잡도로 선택문제(k번째 요소 찾기)를 해결할 수 있는 Median of medians 알고리즘에 대해 알아보겠습니다!
# 동작 원리
Median of medians 알고리즘은 총 4단계의 과정을 통해 설명할 수 있습니다!
1. 5개씩 자르고 5개 중에서 median 찾기
데이터를 각각 5개씩 분할한 후, 5개의 중앙값(m, median)을 찾아준다

2. Median of medians 찾기
Median of medians 을 찾아 m*로 표시한다
B -> m*보다 큰 값들로 이루어진 집합
C -> m*보다 작은 값들로 이루어진 집합
(A,D는 m* 보다 큰지 작으지 알 수 없음)
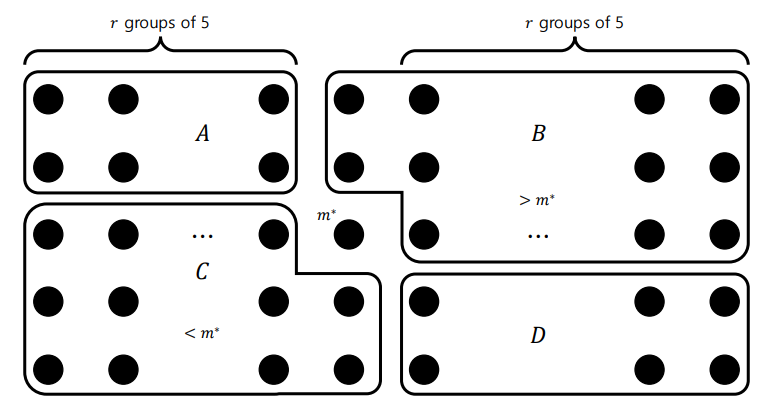
총 데이터의 크기 n은 다음과 같이 표기 가능하다
n = 가로 X 세로 = (2r+1) X 5
즉, n = 5(2r+1)
(추후 성능분석시 필요함)
3. S1, S2 생성 (S1 < m* < S2)
S1 = C ∪ ((A ∩ D) 중에서 m*보다 작은값)
S2 = B ∪ ((A ∩ D) 중에서 m*보다 큰값)
4. 찾고자 하는 k번째 값(k번째로 작은 값)과 비교
k = ㅣS1ㅣ(S1의 크기) +1 인 경우, k는 m*이므로 m*를 그대로 호출
k <=ㅣS1ㅣ 인 경우, 재귀적으로 S1에서 k찾기
k >ㅣS1ㅣ 인 경우, 재귀적으로 S2에서 k -ㅣS1ㅣ-1 찾기
(전체에서 k번째값을 찾는것은 S2에서는 k -ㅣS1ㅣ-1번째 값을 찾는것과 동일함)

# 성능분석 - 최악의 경우
Median of medians 알고리즘을 이용하여 n의 수를 가진 데이터에서 k번째 값을 선택할 시,
최악의 경우(worst) 비교횟수를 계산해 봅시다!
즉, 목표는 w(n)찾기
(w(n) = n의 수 입력에 대한 k번째 값 선택의 최악의 경우 비교횟수)
각 단계별로 비교횟수를 계산해보겠습니다
1. 5개씩 자르고 5개 중에서 median 찾기
데이터를 각각 5개씩 분할하였으므로 총 n/5개의 집합
5개의 값에서 중앙값을 찾는 연산의 비교횟수는 6
6 X (n/5)
즉, 6/5n
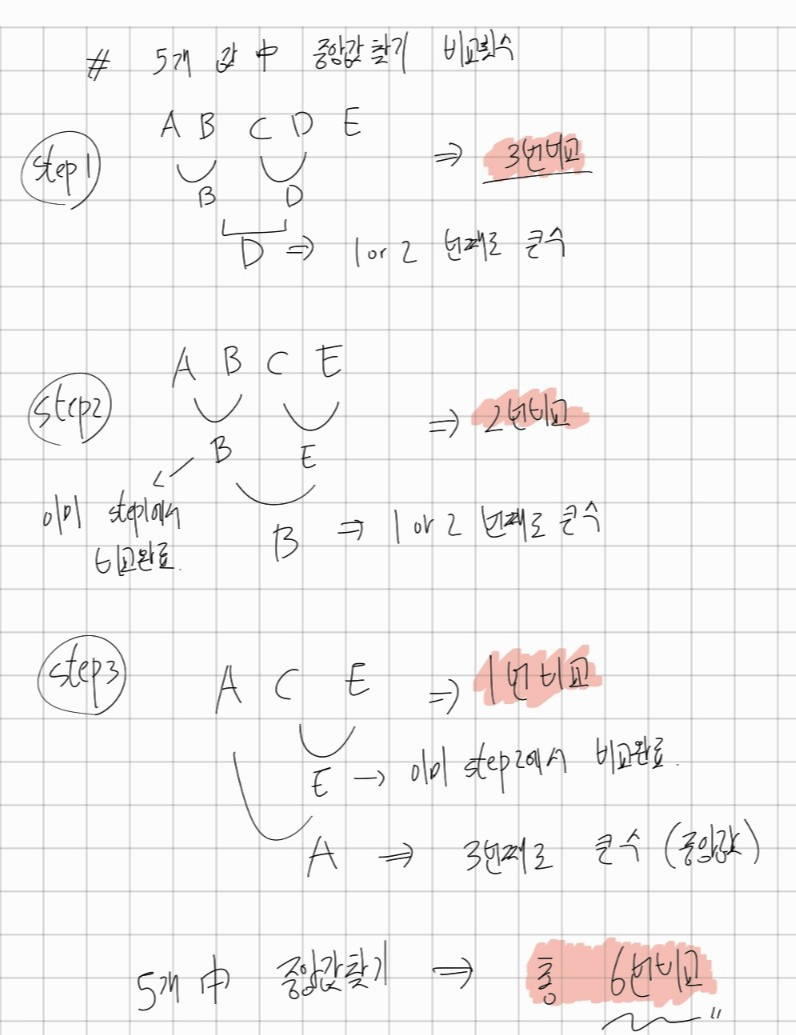
2. Median of medians 찾기
전체 데이터 n중에 중앙값만 선택된 집합인 n/5에서의 최악의 비교횟수 재귀적으로 호출
w(n/5)
3. S1, S2 생성 (S1 < m* < S2)
A, D 영역의 값 모두 m*와비교
2r + 2r = 4r
4. 찾고자 하는 k번째 값(k번째로 작은 값)과 비교
최악의 경우만 고려하므로 Best case인 k = ㅣS1ㅣ인 경우는 제외,
나머지 경우 비교시 재귀적으로 반복
특히 Worst case는 A, D집합의 값 모두가 m*보다 작거나 큰 경우이므로
A+D+(C or D) = 2r + 2r + 3r+2 = 7r+2
7r+2 만큼의 값을 재귀적으로 호출하여 비교
w(7r+2)
최종 w(n)은 1,2,3,4 과정을 모두 더함
n = 5(2r+1)
대략 10r = n
4r = 0.4n
w(n) = 6/5n + w(n/5) + 4r + w(7r+2)
<= 1.2n + 0.4n + w(0.2n) + w(0.7n)
<= 1.6n +w(0.2n) + w(0.7n)
해당식은 재귀식(recursive) 이므로 풀어서 쓰면,
w(n) = 1.6n +w(0.2n) + w(0.7n)
n에 0.2n 입력
w(0.2n) = 1.6 X 0.2n +w(0.2 X 0.2n) + w(0.7 X 0.2n)
n에 0.7n 입력
w(0.7n) = 1.6 X 0.7n +w(0.2 X 0.7n) + w(0.7 X 0.7n)
w(n) = 1.6n + 1.6 X 0.2n +w(0.2 X 0.2n) + w(0.7 X 0.2n) + 1.6 X 0.7n +w(0.2 X 0.7n) + w(0.7 X 0.7n)
이런식으로 재귀식을 풀어주면 아래와 같이 도식화할 수 있다
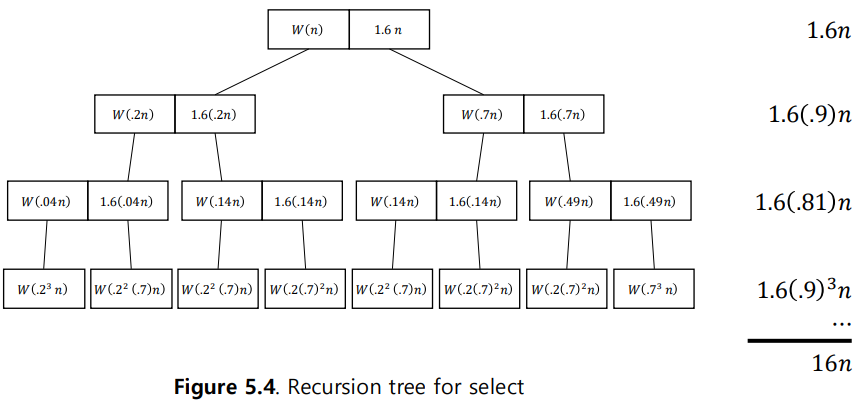
1.6n + 1.6X0.9n + 1.6X(0.9)^2n + 1.6X(0.9)^3n + ...
등비수열 합공식을 이용하여 계산하면,
a = 첫항
r = 공비
a/1-r = 1.6n/1-0.9 = 16n
w(n) <= 16n
즉, Median of medians 알고리즘의 최악의 경우(worst) 에는 16n = O(n) 선형시간만에 선택문제를 해결할 수 있다
최근에는 최악의 경우 16n -> 5.4n -> 2.95n까지 줄인 알고리즘도 개발됐다고 하네욥,,,,
# reference
컴퓨터 알고리즘. (2006). 대한민국: 도서출판 홍릉(홍릉과학출판사).
Baase, S., Van Gelder, A. (1999). Computer Algorithms: Introduction to Design and Analysis, 3rd Edition. 인도: Addison-Wesley.
'Algorithm > 알고리즘 이론(Algorithm theory)' 카테고리의 다른 글
| 힙 정렬(Heap Sort) (1) | 2024.12.01 |
|---|---|
| 쉘 정렬(Shell Sort) (0) | 2024.11.30 |
| 정렬 알고리즘의 안정성(Stability) (0) | 2024.11.29 |
| 다익스트라 (Dijkstra) 알고리즘 (1) | 2024.11.28 |
| 위상 정렬(Topological Sort) (1) | 2024.11.27 |



