힙 정렬(Heap Sort)

오늘은 비교정렬 중 하나인 힙 정렬(Heap Sort)에 대해 알아보겠습니다

힙 정렬은 힙 구조를 이용하여 정렬을 수행하는데욥 힙구조란 무엇일까요?

 

# 힙(Heap) 구조란?

완전 이진 트리(Complete Binary Tree)의 일종인데욥

(왼->오, 위->아래 순번끊김 없는 트리)

 

우선순위 큐(Priority Queue)에도 사용되는 구조입니다!

https://hipposdata.tistory.com/104

우선순위 큐 구현 (PriorityQueue, Heap)

 

힙 구조는 2가지 종류가 있는데욥

 

최대 힙 (Max-Heap)

부모 노드의 값이 자식 노드의 값보다 크거나 같은 구조

즉, 루트 노드에 최댓값이 위치

 

최소 힙 (Min-Heap):

부모 노드의 값이 자식 노드의 값보다 작거나 같은 구조

즉, 루트 노드에 최솟값이 위치

 

# 동작과정 

힙정렬은 2가지 단계로 이루어지는데욥 최초 데이터를 힙구조로 만든 후, 힙구조에서 루트노드(최댓값 or 최솟값)을 하나씩 제거하며 뒤쪽 or 앞쪽부터 채워넣으면서 정렬을 실시합니다

 

1. 힙구조 생성: 최초 데이터를 힙구조로 변형(Heapify)

2. 정렬수행: 루트노드(최댓값 or 최솟값)를 배열의 끝 or 처음으로 이동한 후, 배열 크기를 줄여가며 나머지 부분을 다시 힙 구조로 만듦

 

 

구체적인 예시를 통해 알아보겠습니다

71, 49, 92, 55, 38, 82, 72, 53 총 8개의 수를 오름차순으로 정렬하겠습니다

 

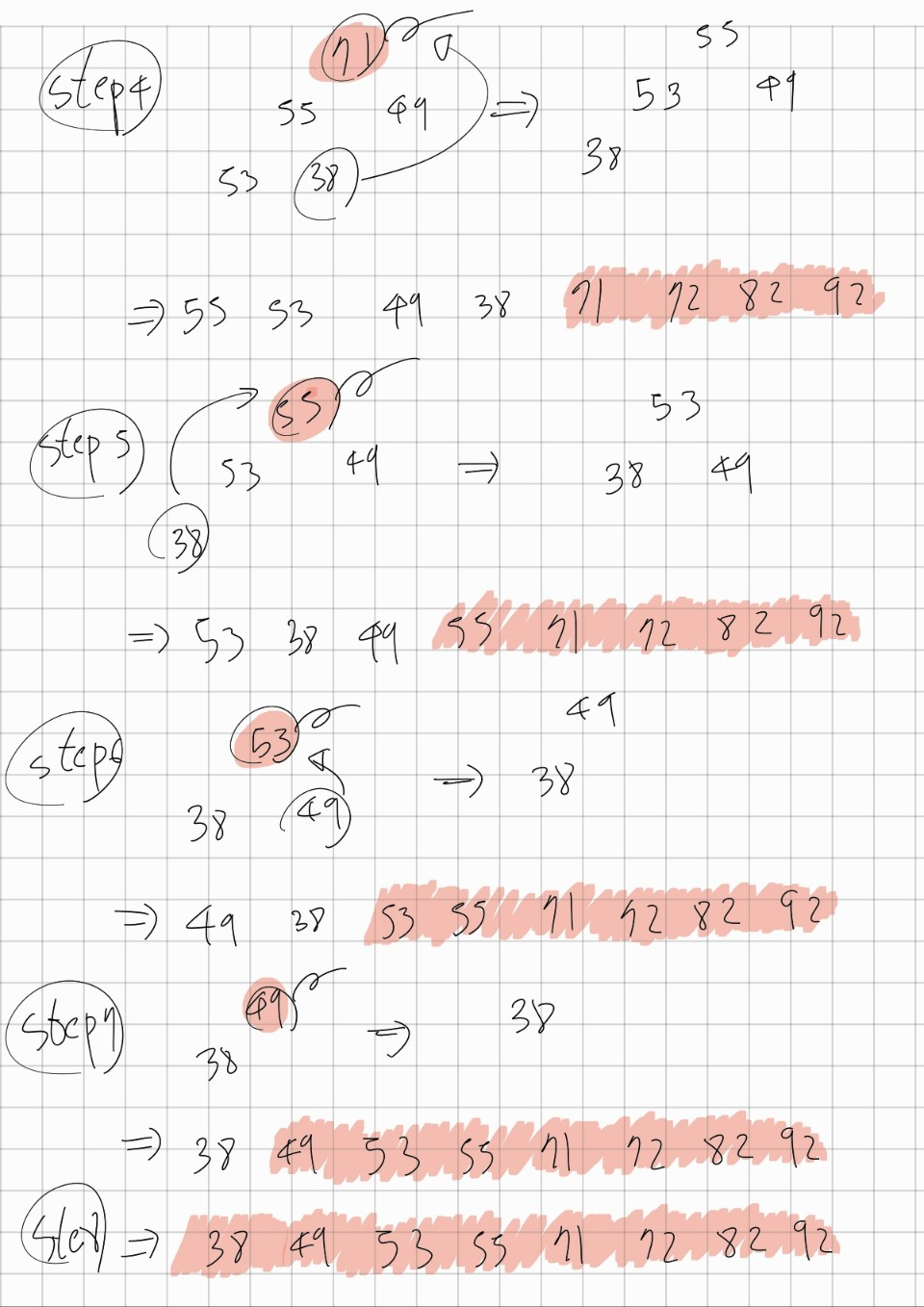
# Python 코드

# 힙 정렬 함수

def heapSort(arr):      

    n = len(arr)  # 배열의 길이를 저장

    print("i=", 0, arr)

    # 배열을 힙 구조로 변환 (Max Heap 생성)

    for i in range(n // 2, -1, -1):  # 배열의 중간부터 시작해 역순으로 힙화

        heapify(arr, n, i)  # 힙 조건을 만족하도록 수정

    print("i=", i, arr)

    # 힙 정렬 수행

    for i in range(n - 1, 0, -1):  # 마지막 원소부터 첫 번째 원소까지 처리

        arr[i], arr[0] = arr[0], arr[i]  # 가장 큰 원소(루트)를 배열의 끝으로 이동

        heapify(arr, i, 0)  # 나머지 부분 배열을 다시 힙 구조로 변환

        print("i=", i, arr)

# 힙구조 생성 (heapify)

def heapify(arr, n, i):    

    largest = i  # 현재 노드를 가장 큰 노드로 가정

    l = 2 * i + 1  # 왼쪽 자식 노드의 인덱스

    r = 2 * i + 2  # 오른쪽 자식 노드의 인덱스

    # 왼쪽 자식 노드가 현재 노드보다 크면 largest 업데이트

    if l < n and arr[i] < arr[l]:

        largest = l

    # 오른쪽 자식 노드가 largest보다 크면 largest 업데이트

    if r < n and arr[largest] < arr[r]:

        largest = r

    # 가장 큰 노드가 현재 노드가 아니라면 교환 후 재귀 호출

    if largest != i:  

        arr[i], arr[largest] = arr[largest], arr[i]  # 교환

        heapify(arr, n, largest)  # 교환된 하위 트리에 대해 재귀적으로 힙 조건 검사

 

# 성능분석 - 시간복잡도

힙정렬의 2단계 각각의 시간복잡도를 살펴볼 수 있는데욥

1. 최초 힙구조 생성 -> n(모든 데이터) X logn(힙구조로 변경)  =  O(nlogn)

2. 정렬수행-> n-1(데이터 하나씩 떼고) X logn(힙구조로 변경)  = O(nlogn)

 

즉,  O(nlogn) + O(nlogn) =  O(nlogn)

# reference

파이썬 자료구조와 알고리즘: for beginner. (2021). 대한민국: 한빛아카데미.

컴퓨터 알고리즘. (2006). 대한민국: 도서출판 홍릉(홍릉과학출판사).

Baase, S., Van Gelder, A. (1999). Computer Algorithms: Introduction to Design and Analysis, 3rd Edition. 인도: Addison-Wesley.