Hippo's data
[시계열 분석] ARIMA Model 본문
해당 포스팅은 김성범 교수님의 ARIMA 모델 개요 - Part 1 강의를 기반으로 작성되었습니다!
https://www.youtube.com/watch?v=ma_L2YRWMHI
-> AR,MA,ARMA 모델 구현 위해 데이터가 stationary 해야함
그렇다면 stationary / Nonestationary 란 무엇일까?
# Stationary Process(정상 프로세스)
→ 안정되어 있는 상태
→ 시간에 관계없이 평균과 분산이 일정한 시계열 데이터
→ 시간이 지나도 통계적 특성(평균, 분산, 자기상관관계)이 변하지 않음

# Nonestationary Process (비정상 프로세스)
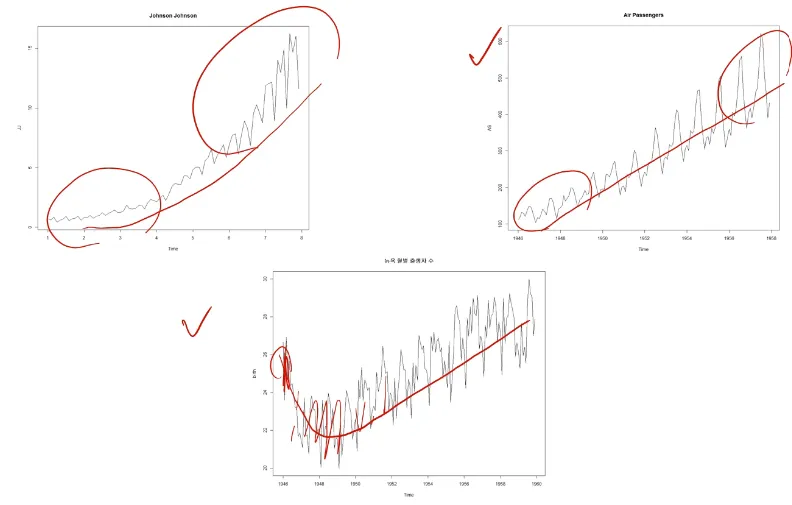
즉, 데이터가 정상성 만족하지 않음
= 시간에 따라 데이터 속성이 변함
= 모델의 매개변수가 변함
= 각 시점마다 계수(coefficient)가 변하므로 과거값으로 미래값을 도출할 수 없음
= 모델 사용 불가
# 정상성 확인 Stationary
복잡한 데이터 → 눈으로 판단하기 힘듦
ADF 테스트(단위근 검정 Unit Root test) 진행
통계값
비정상적(non-stationary) 통계값 -1~1 이내 (0에 가까울수록 강한 비정상성 )
정상적(stationary) 통계값 -1~1 바깥 (보통 큰 음수값 -> 정상적)
p-value
→ p-value 0.05 이내 → 데이터 stationary 하다는 귀무가설 기각 O
귀무가설(H0): 시계열 데이터가 비정상적(non-stationary)이다.
대립가설(H1): 시계열 데이터가 정상적(stationary)이다.
or
ACF(Autocorrelation Function) plot으로 확인
→ x축 lag / y축 Autocorrelation (자기 자신, 자기자신 이전 데이터와의 correlation)
lag1 : 현재 데이터와 한시점 미룬 데이터와의 차이
lag2 : 2시점 미룬(shift)
…
lag20 : 20시점 미룬(shift)
ACF(Autocorrelation Function) plot 해석
일정한 패턴 X / 갑자기 증감 → stationary
일정한 패턴 O / 전반적으로 천천히 감소 → Nonestationary

-> Stationary 만족

-> ACF plot 천천히 감소 -> Nonestationary

-> ACF plot 전반적으로 감소 추세 -> Nonestationary
### PACF(Partial Autocorrelation Function, 편자기상관함수)
-> ACF는 각 지연된(lag) 값들의 상관관계를 측정했다면,
PACF는 각 지연된(lag) 값들 사이의 영향을 제거한 후 해당 값들의 상관관계(편자기상관관계, partial autocorrelation) 측정
예) y_t = 0.3y_t-1 + 0.2y_t-2
ACF -> y_t, y_t-2간의 자기상관관계 측정
PACF -> y_t-1이 y_t, y_t-2 둘다 영향을 미친다는 것을 고려 -> 교란변수(confounding variable) 영향 제거하여 자기상관관계 측정
즉, ACF가 간접적인 영향까지 모두 고려 / PACF는 순수한 직접적 영향만을 측정
< AR, MA, ARIMA Model>
# Autoregressive (AR) Model - 자기회귀모델
AR(p) p: 과거 관측값 수

→ Models that use lags of the dependent variable as independent variables
→ y_t의 과거 lag된 변수들로 회귀모델 생성
y 자기자신으로 모델링하므로 오차항들이 서로 독립X
→ 파이추정(계수값, 파라미터)→ 최소제곱법(OLS) 으로 추정 X
stationary한 데이터의 ACF plot이 느린 감쇄 or 사인(sin) 곡선 패턴 -> 자기회귀(Autoregressive)과정 있을 가능성 높음
-> PACF확인, Autoregressive Model 적용
→ AR(p) : p는 PACF plot을 그린 후, p번째 시차(lag) 이후로 모든 자기상관이 0에 가까워지는 부분(신뢰구간 선 이내 = 통계적 유의미하지 않는 부분) 찾기, 해당 부분 전의 값이 p(통계적으로 유의한 p의 값)
# Moving Average (MA) Model - 이동평균모델
MA(q) q: 과거 오차항 수
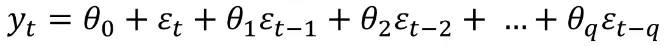
→ Models that use past errors that follow a white noise distribution as explanatory variables.
→ y_t의 과거 error 변수들로 회귀모델 생성
→ MA(q) :q는 ACF plot을 그린 후, q번째 시차(lag) 이후로 모든 자기상관이 0에 가까워지는 부분(신뢰구간 선 이내 = 통계적 유의미하지 않는 부분) 찾기, 해당 부분 전의 값이 q(통계적으로 유의한 q의 값)
### 앞으로 q단계 데이터까지만 유효하게 예측
-> 롤링 예측(Rolling Forecast)으로 q단계 넘어가는 예측도 진행
예) MA(2) 모델 q = 2, 기간 = 50
51,52번째 예측-> 1~52로 새롭게 모델 훈련
-> 53,54번째 예측 -> 1~54로 새롭게 모델 훈련 (최종 예측기간까지 반복)
(q가 2라고 꼭 +2까지 훈련할 필요 없음 +1 or +2 가능)
# Autoregressive and Moving Average (ARMA) Model

→ AR + MA
→ y_t의 과거 lag된 변수들(p개) + 과거 error 변수들(q개)로 회귀모델 생성
stationary한 데이터의 ACF, PACF plot이 느린 감쇄 or 사인(sin) 곡선 패턴
= 유의한 계수가 존재하다가 갑자기 유의하지 않게되는 명확한 지연(lag) 시점 확인 X
-> 자기회귀이동평균(Autoregressive and Moving Average)과정 가능성 높음 -> ARMA Model 적용
# Autoregressive Integrated Moving Average (ARIMA) Model
Autoregressive(AR) Integrated(I) Moving Average(MA)
→ ARIMA
AR(p) / I(d) / MA(q)
→ ARIMA (p,d,q)
p → 과거 관측값 수 / AR model
d→ differencing(차분) 수
q→ 과거 오차항 수 / MA model
# Differencing(차분)
Nonestationary → stationary 방법
Differencing(차분) : 현 시점 데이터에서 d시점 이전 데이터를 뺀 것
1차 차분→ t 시점 1시점 전(shift)의 데이터와의 차이
2차 차분→ t 시점 2시점 전(shift)의 데이터와의 차이
…
d차 차분 → t 시점 d시점 전(shift)의 데이터와의 차이
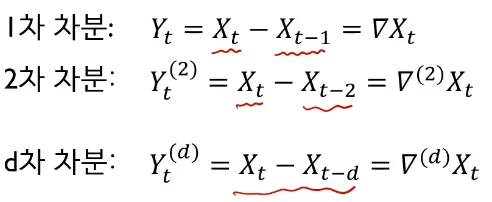
### 초기 시점 t=0는 t=-1이 존재하지 않으므로 (이전시점 존재X) 데이터 요소 하나 손실됨
### 차분 후 최종 예측 후 예측값을 역변환(적분, Integration) 해줘야함 (AR, MA, ARMA 모델 해당함 / ARIMA model은 역변환 필요없음)
# ARIMA - Order of Differncing / 차분 수 판단
오리지널 데이터 stationary / Nonestationary 판단
1. stationary → 차분(Differencing) 필요없음
2. Nonestationary →
일정한 증/감 → 1차차분 (대부분)
복잡한 패턴 → 2차차분
→ 대부분의 데이터는 2차차분으로 충분함
→ 3차차분이상 가는 데이터는 ARIMA 모델 적합하지 X 데이터로 판단

예제) 1st Differencing (1차차분)
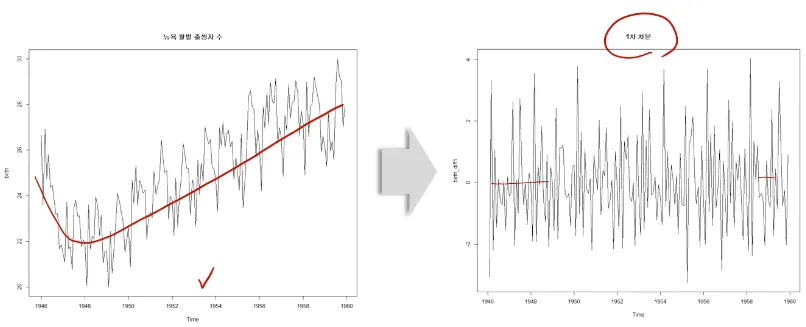
예제) 2st Differencing (2차차분)

→ 1차분으로도 충분함 → 굳이 2차차분 필요 X
→ ACF(Autocorrelation Function) plot 확인

→ stationary 만족
<요약>
AR,MA,ARMA 모델 적용 위해 데이터가 stationary 해야함
stationary 확인 → ACF(Autocorrelation Function) plot
AR,MA,ARIMA model 특성
Nonestationary → 차분(Differencing) 진행
'Time Series Analysis (시계열 분석)' 카테고리의 다른 글
| [TS] 시계열 용어 정리 (0) | 2026.01.31 |
|---|---|
| [TSF] 시계열 데이터 교차 검증(Cross-Validation) 전략 (0) | 2025.11.09 |
| [TSF] 예측 스텝 전략 (0) | 2025.10.27 |
| [시계열 분석] ARIMA Procedure, SARIMA (0) | 2025.02.13 |
| [시계열 분석] Time Series Regression (0) | 2025.02.10 |




