[시계열 분석] Time Series Regression

해당 포스팅은 김성범 교수님의 Time Series Regression 강의를 기반으로 작성되었습니다!

Time Series Regression - Part 1 / 2 /3

https://www.youtube.com/watch?v=7Do_hixXCpc

https://www.youtube.com/watch?v=pxG4ZlHJ570

https://www.youtube.com/watch?v=5QnR4L3KGz4

 

# 시계열 데이터란? (Time series Data)

시간의 흐름에 따라 얻어진 데이터

단위 -> 일,월,달,분기 (Daily, Monthly, Quarterly, Yearly) 등

예) 시간에 따른 제품 판매량/실업자 수/서울시 오염정도 등

 

 

# 시계열 데이터 구성요소

1. 추세 변동 Trend

2. 순환 변동 Cycle

3. 계절변동 Seasonal variations

4. 우연변동 Random fluctuation

 

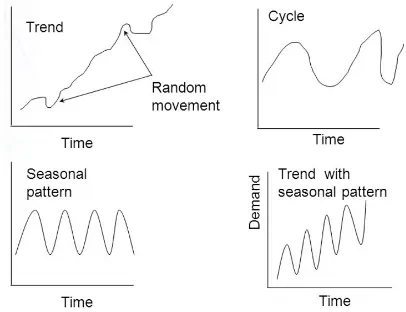
1. 추세 변동 Trend

장기간(보통 1년이상) 관측값 증가(Downward) or 감소(Upward)

 

2. 순환 변동 Cycle

주기적인 변동(계절에 의한것 제외) / 주기(Cycle)가 긴

 

3. 계절변동 Seasonal variations

주별 월별 계절별 주기 / 주기(Cycle)가 짧은 

4. 우연변동 Random fluctuation

- 특정 패턴없는 / 랜덤한 원인

예) 백색잡음 (White noise) - 평균 0 / 분산일정한 시계열 데이터

 

전체 시계열 데이터 = 추세 + 계절성 + 랜덤성

 

 

# 시계열 예측 모델종류

• 시계열 회귀 분석(Time Series Regression)
• 지수평활법(Exponential Smoothing) - 꽤 성능 굿
• ARIMA
• ML(Machine Learning) 예측모델 (Hidden Markov, DNN, … )

 

# 시계열 회귀 분석(Time Series Regression)

일반적인 회귀 모델 

y_t = the value of the series in period t /

TR_t = the trend in period t 

ε_t = the error term in time period t

 

t 시점 값 = 트랜드 + 에러(트랜드 부분으로 설명하기 어려운 부분)

 

 

#  Trend 부분 (TR_t)

 

No Trend: 증가/감소 X // 평균 값(한 값)으로 모든 값을 예측

Linear Trend: 직선형 증가/감소

Quadratic Trend: 곡선형 증가/감소

 

 

# 다항 회귀 모델 (Polynomial)

-> x(input) 변수는 t(시간)뿐임

-> 일반적인 선형회귀 추정법 최소제곱추정량(Least Square Estimator = LSE) 이용

https://hipposdata.tistory.com/75

[회귀분석] 회귀선의 추정

오차(error) 에 대해 독립성 가정

시계열 데이터(Time seriese)는 시간에 따라 얻어짐 -> 각 데이터는 이전 시점의 데이터에 영향을 받게 됨

-> 일반적 최소제곱법 통한 파라미터 추정시 문제될 여지가 있음

-> Autocorrelation(자기상관) 확인

 

 

# Autocorrelation (자기상관) 이란?

correlation -> 두변수 사이의 관계 -1~1

auto -> self

즉, 자기자신과 shift된 자기자신간의 관계

 

# Autocorrelation (자기상관) 유형

1. Positive Autocorrelation

2. Negative Autocorrelation

3. Random Autocorrelation (No Autocorrelation)

 

 

1. Positive Autocorrelation / + + + + -> - - - - - 

 

2. Negative Autocorrelation / + -> - -> + -> - (+,-가 번갈아 등장)

 

3. Random Autocorrelation (No Autocorrelation) / +,- 패턴 없음

 

자기상관성 있는지 유무 판단 -> 오차항 error 확인

-> 표본 데이터에서 오차(모집단 예측값 - 실제값 차이)를 알 수 없음

-> residual 잔차(표본 예측값 - 실제값 차이)로 확인

-> residual plot을 통해가시적으로 확인 불가능한 경우

-> Durbin-Watson Test (검증) 이용 ( first order autocorrelation만 확인 가능)

## first order -> 한시점 미뤄진 shift 데이터 / second order -> 두시점 shift

 

 

# Durbin-Watson Test

1. positive autocorrelation 검정

2. negative autocorrelation 검정

 

1. positive autocorrelation 검정

Hypothesis 가설

H0 : ρ = 0, The error terms are not autocorrelated.

H1 : ρ > 0, The error terms are positively autocorrelated.

 

검정통계량

 

귀무가설 채택  -> 잔차들에서 자기상관성 없음 = 독립이다 -> 검정통계량이 기준값보다 큼

대립가설 채택-> 자기상관성 존재 -> -> 검정통계량이 기준값보다 작음

positive autocorrelation은 같은 구간 계속 나오므로(+++ / ---) 전시점 - 현재시점 잔차 작게됨

즉, 검정통계량 값이 기준값보다 작게되면 대립가설 채택됨 

 

2. negative autocorrelation 검정

Hypothesis 가설

H0 : ρ = 0, The error terms are not autocorrelated.

H1 : ρ < 0, The error terms are negatively autocorrelated.

 

검정통계량

 

 

귀무가설 채택  -> 잔차들에서 자기상관성 없음 = 독립이다 -> 검정통계량이 기준값보다 작음

대립가설 채택-> 자기상관성 존재 -> -> 검정통계량이 기준값보다 큼

negative  autocorrelation은 다른 구간 계속 나오므로(+-+-) 전시점 - 현재시점 잔차 크게됨

즉, 검정통계량 값이 기준값보다 크면 대립가설 채택됨 

표를 이용하여 계산 / p-value 확인

-> postive autocorrelation이 일반적으로 많이 보임 / 파이썬 패키지에서 계산되어 나옴 d-statistics

 

 

#  Seasonal Variation (계절성 분산)

1. constant -> 분산 폭 일정

2. increasing -> 분산 폭이 점점 증가 -> 모델 핸들링 어려움 -> constant하게 바꿔줘야함

 

 

#  How to handle increasing seasonal variations?

일반적 -> 데이터 변환(Transformation)

 

1. Square-Root

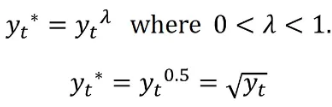
2. Log Trasformation -> 많이 사용됨

 

 

# Modeling Seasonal Variations

 

t 시점 값 = 트랜드 + 계절성 + 에러

 

1. binary variable 

2. trigonometric model

 

 

1. binary variable - 이진 변수

해당 변수에 해당 ->1 나머지 변수는 0

해석 good / 각 변수의 계수값이 그자체로 의미가 있음 ( 11월 변수의 계수는 기준월에 비해 11월 변수가 어떻다~)

 

2. trigonometric model

seoasonal variations을 사인, 코사인(sin, cosin)함수로 표현

-> 주기있는 두 곡선을 이용하여 계절성 설명

-> 해석 hard -> 해석보다는 예측에 사용됨

 

-> simple한 계절성 -> binary variable 이용

-> 복잡한 계절성 ->  trigonometric model 이용

-> 지금까지는 직선형 모델

-> 직선형이 아닌 모델 -> growth curve model 

 

 

# growth curve model - 성장커브

파라미터가 linear(선형) 아님 (덧뺌이아닌 곱/나누기로 연결됨)

-> 파라미터를 linear(선형)로 바꿔줌 -> 로그 취함 (로그곱 -> 로그 합)

 

 

자기상관 유무 판단 -> Residual Plot, Durbin-Watson test (First-order)

자기상관성 X -> LSE 이용 

자기상관성 O -> ARIMA