Hippo's data
[시계열 분석] ARIMA Procedure, SARIMA 본문
해당 포스팅은 김성범 교수님의 ARIMA 모델 개요 - Part 2 강의를 기반으로 작성되었습니다!
https://www.youtube.com/watch?v=P_3808Xv76Q
# Box-Jenkins ARIMA Procedure
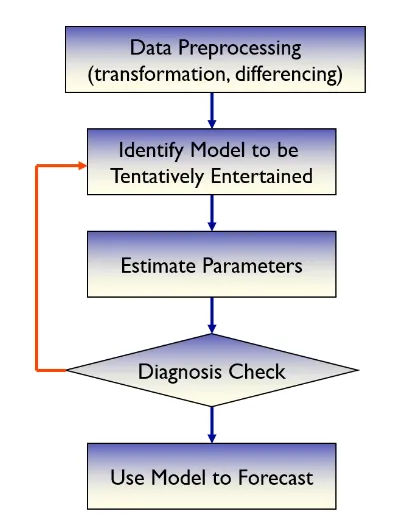
1. Data Preprocessing - 데이터 전처리
2. Identification ARIMA Model - 시범 모델 선택
3. Estimation Parameters - 파라미터 추정
4. Diagnosis Check- Performance Evaluation 모델 진단
5. Forecasting - 최종모델 예측
# 1. Data Preprocessing - 데이터 전처리
ACF(Autocorrelation Function) plot → stationary 정상성 확인
Nonestationary → stationary 변형
->
Transformation( 데이터 변환) - 데이터에 로그함수 적용하여 분산 안정화
or
Differencing(차분) - 현시점에서 과거시점 데이터 뺌 / 추세와 계절성 안정화
-> stationary 정상성 확인방법
https://hipposdata.tistory.com/127
[시계열 분석] ARIMA Model
해당 포스팅은 김성범 교수님의 ARIMA 모델 개요 - Part 1 강의를 기반으로 작성되었습니다!https://www.youtube.com/watch?v=ma_L2YRWMHI -> AR,MA,ARMA 모델 구현 위해 데이터가 stationary 해야함 그렇다면 stat
hipposdata.tistory.com
# 2. Identification ARIMA Model - 시범 모델 선택
Graphical method → 주관적인 방법
→ Autocorrelation Function(ACF) / Partial Autocorrelation Function(PACF) 패턴을 보고 선택
→ 어떤 모델을 사용할지, 차수 등

cut off (절단) → 확 떨어진 / Did out (소멸)→ 천천히 감소, 지수적으로
ACF plot 예제)
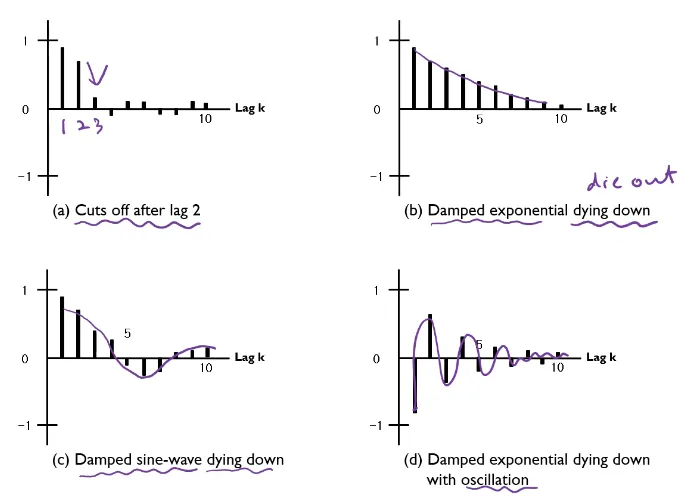
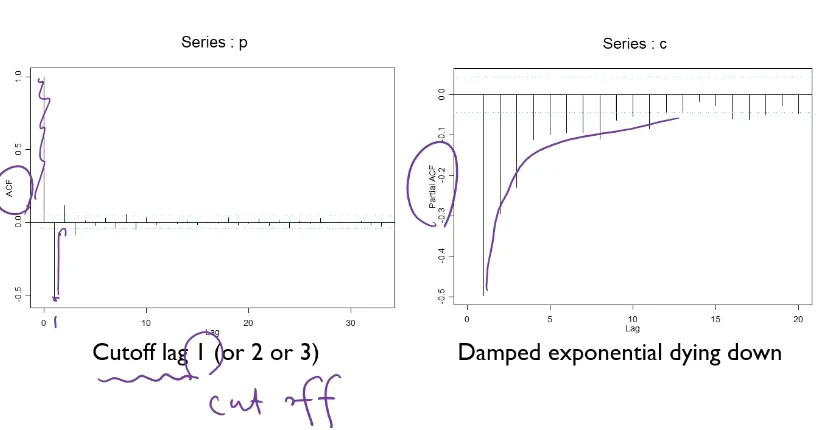
→ plot해석 → q = 1 이후 0으로 확 떨어짐 → MA(1) model 시작
ARIMA(0,1,1) 시범모델 결정
# 3. Estimation Parameters - 파라미터 추정
선택한 모델과 다른 모델들 AIC 값 비교
graphical method의 주관적인 한계가 존재 → 다른 파라미터 모델들도 확인
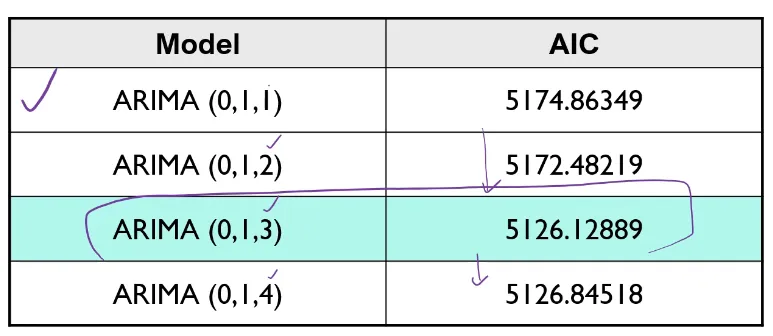
### AIC (Akaike Information Criterion)
Akaike → 일본의 통계학자 **아카이케 히로츠구(Hirotugu Akaike)**의 이름에서 유래
AIC = 2k−2ln(L)
k → 모델의 추정된 파라미터 수 = 모델의 복잡성
L → 모델의 최대 우도(Likelihood) 값 = 모델의 적합도
k 크다 → 파라미터가 많다 = 모델이 복잡하다
L 크다 → 우도가 크다 = 관측된 데이터가 특정 모델에서 나올 가능성이 높다 = 해당 모델이 데이터를 잘 설명한다 = 모델 적합도가 크다
예) 최대우도추정법(MLE):
가정 ) 우도가 클수록 해당 파라미터가 데이터를 잘 설명 → 우도를 최대화하는 파라미터를 찾는 방법
→ k 작을수록, L 클수록 good
→ AIC값 작을수록 good
즉, AIC값 작음 = 높은 적합도, 낮은 복잡성 모델
과대적합(overfitting) -> k(파라미터수) 큼, L(우도값) 큼 -> 적합도는 크지만 복잡도도 크므로 패널티
과소적합(underfitting) -> k(파라미터수) 작음, L(우도값) 작음 -> 복잡도는 작지만 적합도도 작으므로 패널티
-> 과대적합, 과소적합 사이의 균형적인 판단 가능
# 4. Diagnosis Check- Performance Evaluation 모델 진단
residual (모델 예측값 y_hat - 실제값 y) → ACF plot확인
→ bound 안에 40 중 2~3개 이하 넘어간경우 → good
### Upper, Lower bound → residual +- 3 sigma(분산) limit
잔차(residual)의 ACF plot → 40개의 lag 중 bound 밖으로 나가는 값이 2~3개 이하
→ 최종 모델로 결정
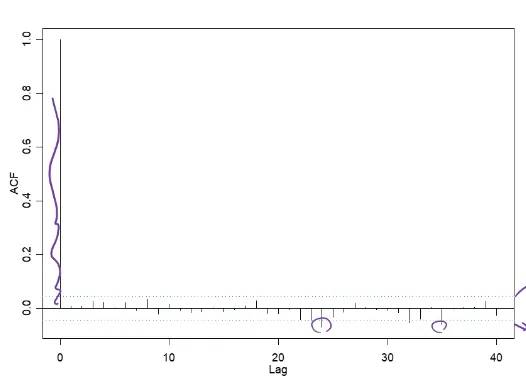
즉, 여러 모델들의 p, d, q 조합 반복문을 통해 고려, AIC 등 평가 점수를 비교하여 최종 모델 결정
# 5. Forecasting - 최종모델 예측
결정된 최종모델 기반으로 최종 예측
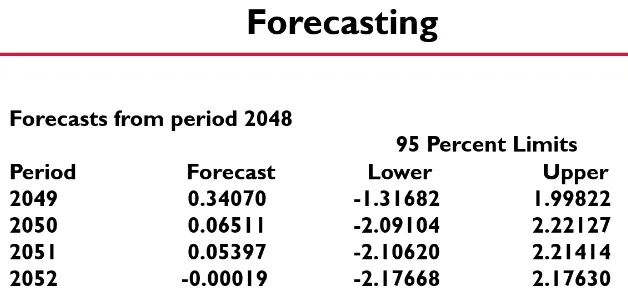
# Seasonal ARIMA Model (SARIMA)
기존 ARIMA + Seasonal(계절 변동) = SARIMA
→ 각 계절에 따른 독립적인 ARIMA 모델이 합쳐진 모형
→ ARIMA(p,d,q)(P,D,Q)s → 계절성 주기 차수 s 추가됨
→ 파라미터 7개

예) s = 12 월별 / s = 4 분기별


'Time Series Analysis (시계열 분석)' 카테고리의 다른 글
| [시계열 분석] ARIMA Model (2) | 2025.02.12 |
|---|---|
| [시계열 분석] Time Series Regression (0) | 2025.02.10 |


