Hippo's data
[Paper review] A Comprehensive Survey of Deep Learning for Time Series Forecasting: Architectural Diversity and Open Challenges 본문
[Paper review] A Comprehensive Survey of Deep Learning for Time Series Forecasting: Architectural Diversity and Open Challenges
Hippo's data 2025. 11. 25. 01:15
오늘 가져온 논문은 시계열 분야 특히 시계열 예측(TSF) 분야를 전반적으로 톺아볼 수 있는 서베이 논문입니다!
해당 논문은 리뷰중심 저널 AIR(Artificial Intelligence Review)에 개재되었습니다!
1. Introduction
2. Background
3. Historical TSF Models
4. New Exploration of TSF Models
5. TSF Latest Open Challenges & Handling Methods
목차는 다음과 같은데욥
시계열(TS)분야 기본적인 배경 지식 부터 시계열 예측(TSF) 분야 모델 발전과정, 최신 연구에서 다루는 주제까지 시계열예측분야(TSF)를 전반적으로 살펴볼 수 있습니다
1. Introduction
Time-Series 분야는 다양한 카테고리로 분류할 수 있습니다
Forecasting, Classification, Anomaly Detection, Foundation Model, Data Processing, Representation Learning, Causality
그중 해당 논문은 TSF(Time-Series Forecasting) 분야를 다루는데요
→ 즉, 순차적인 과거 데이터를 기반으로 미래 값을 예측하는 분야입니다!
하단 그래프에서 확인할 수 있듯이, TSF분야가 점점 핫해지고 있네욥

-> 2020년부터 2024년까지 상위 AI 및 머신러닝 학회에서 발표된 시계열 예측(TSF) 관련 논문의 수
-> 2020년부터 2024년까지 TSF 관련 논문 수가 폭발적으로 증가
2. Background
2.1 시계열 예측(TSF) 문제 정의
2.2 시계열 데이터의 특징
2.3 TSF Datasets
2.4 Evaluation Metrics
2.1 시계열 예측(TSF) 문제 정의
1) 입력 변수의 수
- 단변량 시계열 예측 (Univariate Time Series Forecasting, UTSF)
-> 하나의 변수만을 사용하여 미래 값을 예측
예) 과거 기온 데이터만을 이용해 내일 기온을 예측
- 다변량 시계열 예측 (Multivariate Time Series Forecasting, MTSF)
-> 여러 변수를 동시에 사용하여 미래 값을 예측
예) 기온, 습도, 풍속 등 다양한 변수를 고려하여 내일 기온을 예측

2) 예측 범위
- 단기 시계열 예측 (Short-Term Time Series Forecasting, STSF)
-> 가까운 미래에 대한 예측 - 즉각적인 운영 계획이나 단기 의사 결정
- 장기 시계열 예측 (Long-Term Time Series Forecasting, LTSF)
-> 멀리 떨어진 미래(수개월, 수년 이상)에 대한 예측 - 장기 전략 계획, 투자 결정, 정책 수립
2.2 시계열 데이터의 특징
- 시간 순서 (Temporal Order)
데이터 포인트가 시간에 걸쳐 일정한 간격으로 기록
- 자기 상관 (Autocorrelation)
현재 시점의 데이터 값이 과거 시점의 자신과 상관 관계를 가지는 것
- 추세 (Trend)
시간이 지남에 따라 데이터가 전반적으로 증가하거나 감소하거나 또는 일정하게 유지되는 장기적인 움직임
- 계절성 (Seasonality)
정해진 기간(예: 일, 주, 월, 년)마다 반복적으로 나타나는 단기적인 패턴
- 이상치 또는 노이즈 (Outliers or noise)
일반적인 패턴에서 크게 벗어나는 비정상적인 데이터 포인트
- 불규칙성 (Irregularity)
시계열 데이터에서 예측하기 어려운 무작위적인 변동 요소, 다른 패턴들로 설명할 수 없는 부분
- 주기 (Cycles)
계절성보다 긴 패턴를 가지며, 경제 주기와 같이 다소 불규칙한 간격으로 반복되는 패턴
- 비정상성 (Non-stationarity)
시계열 데이터의 통계적 특성(예: 평균, 분산)이 시간에 따라 변하는 현상, 많은 통계 모델은 데이터의 정상성(stationarity)을 가정하므로, 비정상성 데이터는 안정적인 모델 구축을 어렵게 함
2.3 TSF Datasets
TSF 모델들을 훈련하고 평가하는 데 자주 사용되는 공개 벤치마크 데이터셋
에너지, 교통, 날씨, 금융, 질병 등 다양한 도메인

2.4 Evaluation Metrics
1). 확정론적 모델(Deterministic Models)
-> 예측된 단일 값이 실제 관측된 값과 얼마나 "정확하게" 일치하는지 (단일 예측값 출력)
예) 내일 주가는 10,000원이 될 것이다
- 오차 기반 지표 (Error-Based Metrics): 예측값과 실제값의 차이를 측정
MAE (Mean Absolute Error), MSE (Mean Squared Error),
MAPE (Mean Absolute Percentage Error)
sMAPE (Symmetric Mean Absolute Percentage Error)
- 설명된 분산 지표 (Explained Variance Metrics): 모델이 데이터의 분산을 얼마나 잘 설명하는지 평가
R² (Coefficient of Determination)
Adjusted R² (Adjusted Coefficient of Determination)
EVS (Explained Variance Score)
- 모델 선택 지표 (Model Selection Metrics): 모델의 적합도와 복잡성 간의 균형을 고려하여 최적 모델을 식별
AIC (Akaike Information Criterion)
BIC (Bayesian Information Criterion)
HQC (Hannan-Quinn Criterion)
2) 확률론적 모델(Probabilistic Models)
-> 예측된 분포나 구간이 실제 값의 불확실성을 얼마나 잘 포착하고 커버하는지
다양한 가능성의 분포(distribution forecast), 신뢰 구간(prediction interval)을 예측
예) 내일 주가는 9,500원에서 10,500원 사이일 확률이 90%이다
- 오차 기반 지표 (Error-Based Metrics) : 예측과 실제의 차이를 측정
Logarithmic Score (Log Score) -> 예측 확률과 실제 결과 간의 차이를 로그 함수로 평가
CRPS (Continuous Ranked Probability Score) -> 분포 예측의 정확도를 측정
- 구간 지표 (Interval Metrics): 예측의 신뢰 구간을 평가
PICP (Prediction Interval Coverage Probability) -> 관측값이 예측 구간 내에 포함되는 비율을 측정
PIW (Prediction Interval Width)
Quantile Metrics (Quantile Loss / Pinball Loss)
Sharpness Metrics (Sharpness)
3. Historical TSF Models
TSF 모델 발전과정
3.1 Conventional Methods (Before Deep Learning)
3.2 Fundamental Deep Learning Models
3.3 The Prominence of Transformer-based Models
3.4 Uprising of Non-Transformer-based Models

3.1 Conventional Methods (Before Deep Learning)
- 3.1.1 Statistical Models
- 3.1.2 Machine Learning Models
3.1.1 Statistical Models
- Exponential Smoothing (지수 평활) - Brown (1959), Holt (1957), Winters (1960)
- ARIMA (AutoRegressive Integrated Moving Average) - George Box, Gwilym Jenkins (1970)
- SARIMA (Seasonal ARIMA) - George Box, Gwilym Jenkins (1976)
- SARIMAX(SARIMA eXogenous) - George Box, Gwilym Jenkins (1983)
-> 수학적 가정 기반, 단순하고 직관적, 데이터의 기본적인 패턴을 식별하고 해석하는 데 유용
-> 사전에 정의된 선형 관계에 의존하기 때문에 시계열 데이터의 복잡한 비선형 패턴을 학습하는 데 어려움, 대규모 데이터에는 한계
3.1.2 Machine Learning Models
- Decision Trees (의사결정 나무) - 1986년 (Quinlan) / 2013년 (Barlin et al)
- Support Vector Machines (SVM) - 1995년 (Cortes), Support Vector Regression (SVR) - 1996년 (Vapnik et al)
- Gradient Boosting Machines (GBM): - 2001년 (Friedman)
- XGBoost - 2016년 (Chen and Guestrin)
-> 선형 가정에 의존하지 않고 비선형 패턴을 학습하는 데 뛰어난 능력
-> 대규모 데이터셋에서의 예측
3.2 Fundamental Deep Learning Models
- 3.2.1 MLPs: The Emergence and Constraints of Early Artificial Neural Networks
- 3.2.2 RNNs: The first neural network capable of processing sequential data and modeling temporal dependencies
- 3.2.3 CNNs: Extracting key patterns in time series data beyond just images
- 3.2.4 GNNs: Structurally modeling relationships between variables
3.2.1 MLPs: The Emergence and Constraints of Early Artificial Neural Networks
Multi-layer Perceptron(MLP), 역전파(back-propagation) 알고리즘 개발 - (Rumelhart et al, 1986)
-> 비선형 패턴(nonlinear patterns)을 모델링하는 데 강력한 성능
한계점
1) 시간적 종속성 학습의 제한(Limited in learning temporal dependencies)
-> 시간 순서에 따른 정보의 흐름, 이전 상태의 정보를 기억할 수 있는 구조적 메커니즘이 없음
2) 기울기 소실(Vanishing Gradient)
-> 깊은 신경망을 훈련하는 과정에서 기울기(gradient)가 점차적으로 소실되어 정보가 제대로 전달되지 않는 문제가 발생, 이로 인해 모델 학습이 어려워짐
3) 데이터 및 컴퓨팅 자원 부족(Lack of data and computing resources)
3.2.2 RNNs: The first neural network capable of processing sequential data and modeling temporal dependencies
RNNs(Recurrent Neural Networks) - (Hopfield, 1982)
-> 시계열 데이터와 같이 순서가 중요한 순차 데이터를 처리하기 위해 고안
-> MLPs의 한계를 극복하고 시간적 의존성(temporal dependencies)을 효과적으로 모델링 - 이전 시점의 은닉층 출력이 현재 시점의 입력으로 다시 사용
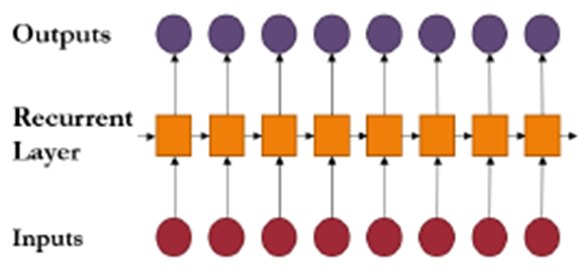
한계점
- 기울기 소실(Vanishing Gradient) - 역전파(backpropagation) 과정에서 기울기(gradient)가 작아지는 현상
- 기울기 폭주(Exploding Gradient) - 역전파 과정에서 기울기 값이 과도하게 커지는 현상
-> 초기 시간 단계의 정보가 나중 시간 단계까지 효과적으로 전달되지 못함
-> 즉, 모델이 장기 의존성(long-term dependencies)을 학습하는 데 어려움
- 병렬 처리의 어려움(Difficulty in Parallel Processing)
Overcoming the Limitations of RNNs : 장기 의존성 문제(long-term dependencies) 해결
LSTM (Long Short-Term Memory) – (Hochreiter and Schmidhube, 1997)
-> Cell State, 게이트 메커니즘
-> 입력(input), 출력(output), 망각(forget) 게이트라는 메커니즘을 사용하여 중요한 정보를 장기간 보존하고 불필요한 정보는 버림
GRU (Gated Recurrent Unit) - Cho et al, 2014)
-> LSTM의 대안 / LSTM보다 단순한 구조(업데이트, 리셋 게이트)
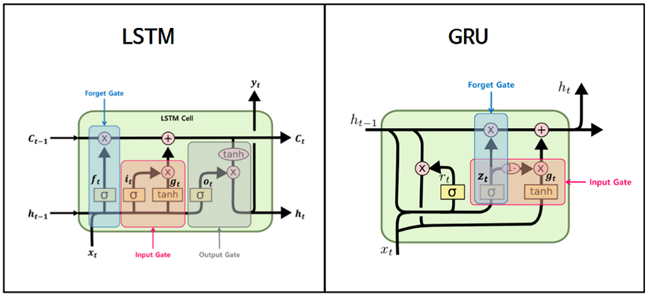
Notable RNN Variants (RNN 변형 모델) : LSTM과 GRU의 성공을 기반으로, 더 복잡한 시계열 특성을 다루기 위한 다양한 접근 방식 개발
Dilated RNN (Chang et al, 2017)
DA-RNN (Dual-stage Attention-based RNN) (Qin et al, 2017)
MQ-RNN (Multi-Quantile RNN) (Wen et al, 2017)
-> 트랜스포머가 등장하기 전까지 시계열 데이터를 다루는 강력한 도구로 활용
3.2.3 CNNs: Extracting key patterns in time series data beyond just images
The Emergence and Early Applications of CNN
Neocognitron (Fukushima, 1980) - 컨볼루션(convolutional)층과 특징의 위치 변화에 강건하게 만드는 풀링(pooling)층 아이디어 제안
LeNet의 발전 (LeCun et al, 1998) - Neocognitron의 개념을 발전시켜 널리 알려진 CNN 아키텍처 확립
-> 초기 CNN 기반 모델들은 주로 이미지 데이터(2D) 처리에 집중
Attempts to Apply CNNs to Time Series Data
-> CNN 모델이 시계열 데이터와 같은 1차원 순차 데이터를 처리할 수 있는 잠재력 인식
1D CNN 등장: 시계열 데이터의 로컬 패턴을 학습하기 위해 1차원 컨볼루션 필터(one-dimensional convolutional filters) 도입
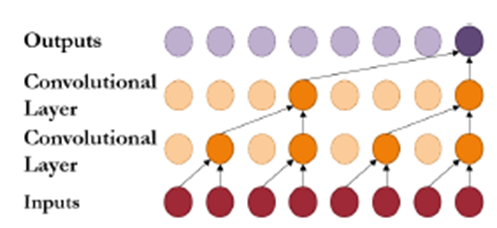
WaveNet(Van Den Oord et al, 2016) : 1D 컨볼루션과 dilated 컨볼루션을 활용,음성 신호(speech signals)를 모델링
-> 오디오 신호의 장기적인 의존성을 효과적으로 포착할 수 있음을 보여줌
TCN(Temporal Convolutional Networks)
-> (Bai et al, 2018) -> 여러 층의 1D 컨볼루션 네트워크로 구성
CNN and RNN Hybrid Models
RNN 계열 모델(특히 LSTM, GRU) -> 시계열 데이터의 장기적인 시간 의존성을 모델링하는 데 강점
CNN 계열 모델 -> 1D 컨볼루션을 통해 시계열 데이터의 로컬 패턴을 추출하는 데 유용
-> 일반적으로 CNN이 먼저 시계열 데이터에서 복잡한 특징(로컬 패턴)을 추출
-> 추출된 특징들을 LSTM과 같은 RNN이 입력받아 시간적인 의존성(temporal dependencies)을 학습
주요 하이브리드 모델
DCRNN (Diffusion Convolutional Recurrent Neural Network) (Li et al, 2018) :
-> Diffusion Convolution을 사용하여 공간적 의존성을 학습, Gated Recurrent Units (GRU)를 사용하여 시간적 의존성을 모델링
TPA-LSTM (Temporal Pattern Attention LSTM) (Shih et al, 2019) :
-> CNN과 LSTM에 Temporal Pattern Attention (TPA) 메커니즘을 추가
-> CNN이 로컬 패턴을 추출하고, LSTM과 어텐션 메커니즘의 조합이 중요한 시간적 패턴을 포착하도록 설계
3.2.4 GNNs: Structurally modeling relationships between variables
The Emergence and Slow Growth of GNN-Based Models
Graph Neural Networks (GNNs) - (Scarselli et al, 2008)
-> 그래프(Graph) 구조의 데이터를 처리하기 위해 개발
Development and Expansion of GNN Applications
Graph Convolutional Networks (GCNs) (Kipf and Welling, 2017)
-> 그래프 구조에서 convolution 연산을 통해 노드 특성을 학습
-> 다변량 시계열 데이터에서 변수(채널) 간의 관계와 시간적 지역성을 학습하는 데 더욱 효과적
ST-GCN (Spatio-Temporal Graph Convolutional Networks) (Yan et al, 2018) :
-> GCN과 RNN을 결합하여 시공간 데이터의 복잡한 패턴을 학습
GAT (Graph Attention Networks) (Veliˇckovi´c et al, 2018):
-> 어텐션 메커니즘을 사용하여 노드 간의 관계를 학습
DyGNN (Dynamic Graph Neural Networks) (Ma et al, 2020): 시간에 따라 변화하는 그래프 구조를 학습
TGN (Temporal Graph Networks) (Rossi et al, 2020):
-> 노드의 시간적 상태 변화를 추적하고, 시간에 따라 중요도가 달라지는 인접 노드의 정보를 학습
3.3 The Prominence of Transformer-based Models
- 3.3.1 Transformer Variants
- 3.3.2 Limitation of Transformer-based Models
Transformer (Vaswani et al, 2017)
-> 자연어 처리(NLP) 분야의 복잡한 시퀀스-투-시퀀스(sequence-to-sequence) 작업을 위해 개발된 모델
시계열 예측(TSF) 분야에서의 부상 : 기존 순환 신경망(RNN) 기반 모델들이 가진 한계 극복
병렬 처리 능력
-> 각 시간 단계의 계산이 이전 단계에 의존하지 않고 동시에 처리될 수 있어, 학습 속도와 효율성이 크게 향상
장기 의존성 학습
-> Self-Attention 메커니즘이 시퀀스 내의 모든 시간 단계 간의 관계를 동시에 고려하여, 멀리 떨어진 데이터 포인트 간의 중요한 장기 의존성(long-term dependencies)을 효과적으로 학습
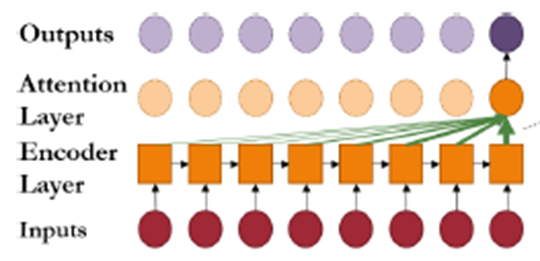
3.3.1 Transformer Variants
장기 시계열 예측(Long-Term Time Series Forecasting, LTSF)에 적용하기 위해 기존 트랜스포머(Transformer) 모델의 한계를 극복하고자 개발된 다양한 변형 모델
기존 트랜스포머의 주요 한계
- 오류 누적
auto-regressive(자기 회귀)한 디코더 특징 -> 이전 예측 값이 다음 예측에 사용되기 때문에 초기 예측 오류가 점차 누적될 수 있음
- 시간 및 메모리 복잡도
셀프-어텐션(Self-Attention) 메커니즘-> O(L^2)
L: 입력 시퀀스 길이 (예: 과거 데이터의 길이)
O(L^2): 시퀀스 길이가 길어질수록 계산량과 메모리 사용량이 제곱에 비례하여 증가
-> 긴 시계열 데이터를 처리할 때 엄청난 계산 비용과 메모리 부담을 초래
시간 및 메모리 복잡도 줄이기
-> 희소 어텐션(Sparse Attention) 메커니즘, 계층적(Hierarchical) 구조를 도입 + 시계열 데이터의 특성(예: 계절성, 트렌드)을 더 잘 반영하기 위한 추가적인 메커니즘을 도입

-> 입력 시퀀스의 모든 토큰(또는 시계열 데이터의 모든 시점)이 시퀀스 내의 다른 모든 토큰과의 관계를 계산
(b) Sparse Self-Attention (희소 Self-Attention)
-> 일부 토큰 간에만 어텐션 관계를 설정
-> O(L^2) -> O(LlogL)
LogTrans (Li et al, 2019), Reformer(Kitaev et al, 2020)
Informer(Zhou et al, 2021),
Autoformer(Wu et al, 2021)
Pyraformer (Liu et al, 2021) , Fedformer(Zhou et al, 2022)
Non-stationary Transformer (Liu et al, 2022)
3.3.2 Limitation of Transformer-based Models
-> 시계열 예측(TSF)에 특화된 Transformer 모델들이 가지고 있는 주요 한계점
1) Efficiency Challenges
Self-Attention 메커니즘의 계산 및 메모리 복잡도
Full Self-Attention O(L^2) -> Sparse Self-Attention O(L log L), O(L)
-> Transformer의 핵심적인 특징이나 성능의 일부를 희생해야 하는 트레이드 오프(trade-off)가 존재
-> MLP(Multi-layer Perceptron), CNN(Convolutional Neural Network) 기반 모델은 일반적으로 선형(O(L)) 또는 그보다 낮은 복잡도
2) Context Window Limited to Current Input
Transformer의 이론적 장점
Self-Attention 메커니즘 -> 입력 시퀀스 내에 있는 모든 토큰들이 서로 직접적으로 정보를 주고받을 수 있음
-> 장기 의존성(long-term dependencies)을 효과적으로 포착
전체 데이터를 넣을 경우의 복잡도 한계 O(L^2) -> 전체 데이터를 한 번에 모델에 넣을 수가 없음
-> 윈도우 길이로 잘라서 넣음 (Context Window)
-> 윈도우 '경계'를 넘어서는 토큰들 간의 관계는 직접적으로 파악할 수 없음
예) 전체 시계열 : [A, B, C, D, E, F, G, H], Context Window length : 4
[A, B, C, D] [E, F, G, H] -> 각 윈도우 내의 관계 파악 가능 / A<->E -> 윈도우 밖의 관계 파악 불가능
-> RNN계열 모델들은 전체 과거를 한 번에 처리할 필요 없이, 현재 입력과 직전의 hidden state만 사용하여 컨텍스트를 보존할 수 있어 긴 시퀀스에 더 효율적으로 작동가능
3) Ineffectiveness of Expanding Input Window Length
-> Transformer 모델에서 입력 윈도우(look-back window) 길이를 늘려도 예측 성능이 개선되지 않거나 오히려 저하되는 현상
일반적인 예측 모델 ->더 많은 과거 데이터(더 큰 look-back window)를 분석할수록 시간적 패턴과 관계를 더 잘 학습하여 예측 성능이 향상될 것으로 기대
Transformer 모델 -> 입력 윈도우 길이를 증가시킬 때 성능이 개선되지 않거나 심지어 저하되는 경향 (Zeng et al, 2023, Zhou et al, 2021, Wen et al, 2023 연구)
노이즈에 과적합 (Overfitting to Noise)
-> Self-Attention 메커니즘 -> 시퀀스 내 모든 토큰 관계 파악 -> look-back window 길어지면, 노이즈를 과도하게 학습
시계열의 특성 미고려
-> Self-Attention(순서 불변성) + Positional Embedding -> 순서 정보를 주입 -> 시계열의 특성(비정상성, 강한 순서 의존성, 복잡한 주기성 등) 고려 한계
3.4 Uprising of Non-Transformer-based Models
-> TSF 분야에서 트랜스포머(Transformer) 모델의 한계가 부각되면서, 기존의 비-트랜스포머 기반 딥러닝 모델들이 다시 주목
트랜스포머 모델의 한계
1) 계산 복잡도 - Self-attention 메커니즘의 점 단위(point-wise) 연산은 시퀀스 길이가 길어질수록 계산량이 제곱(quadratic time complexity)으로 증가
2) 메모리 사용량 - 모든 입력 토큰 쌍 간의 관계 정보를 저장하는 데 상당한 메모리가 필요하여 GPU 메모리가 제한된 환경에서는 적용하기 어려움
3) 장기 의존성 학습: 룩백 윈도우(look-back window)의 길이가 모델의 구조적 용량을 초과하면 장기 의존성을 학습하는 데 어려움
4) 과적합(Overfitting) 위험: 모델의 복잡도가 높아 대규모의 고품질 데이터셋이 필요하며, 데이터가 부족할 경우 과적합으로 인해 모델 성능이 저하될 수 있습니다.
-> Transformer의 계산 복잡도를 줄이고 장기 의존성 학습을 강화하는 방향으로 연구를 지속
-> RNN, CNN, GNN, MLP와 같은 근본적인 딥러닝 모델 재조명

4. New Exploration of TSF Models
-> 최신 TSF 모델들의 새로운 탐구 방향, 발전
4.1 Overcoming Limitations of Transformer
4.2 Growth of Fundamental Deep Learning Models
4.3 Emergence of Foundation Models
4.4 Advance of Diffusion Models
4.5 Debut of the Mamba
4.1 Overcoming Limitations of Transformer
-> 시계열 예측(TSF) Transformer 모델의 한계를 극복하고 성능을 향상시키기 위한 접근 방식
- 4.1.1 Patching Technique
- 4.1.2 Cross-Dimension
- 4.1.3 Exogenous Variable (외인성 변수)
- 4.1.4 Additional Approaches
4.1.1 Patching Technique
-> 입력 시퀀스를 여러 개의 '패치(patch)'로 분할하여 처리
-> 개별 TS 데이터 포인트의 낮은 의미론적 정보 보완
-> 각 패치 내의 지역적(local) 정보를 보존, 시계열 데이터의 특성을 더 잘 반영
-> 처리할 토큰 수가 줄어들어 어텐션 메커니즘의 계산 복잡도 감소
-> PatchTST([Nie et al, 2023]), MTST(Zhang et al, 2024), PETformer(Lin et al, 2024)

# Linear Projection (선형 투영) - Transformer 모델이 처리할 수 있는 고차원의 벡터 표현(임베딩)으로 변환
4.1.2 Cross-Dimension
-> 다변량 TS 데이터에서 변수(채널) 간의 복잡한 상관관계를 효과적으로 모델링하여 예측 정확도를 높임
-> 기존 Transformer 모델은 주로 한 변수의 시간적 어텐션(temporal attention)에 집중하여 채널 간의 상관관계를 효과적으로 포착하지 못함

Cross-Dimension 모델링 진화 단계
-> 각 변수간 상호작용 고려
2) 시간적, 변수적 측면 동시 모델링:
-> 각 변수의 '과거 흐름'과 '변수들 간의 상호작용'을 함께 파악.
Crossformer (Zhang and Yan, 2023) / DSformer (Yu et al, 2023) / CARD (Wang et al, 2024b) / iTransformer (Liu et al, 2024c) / GridTST (Cheng et al, 2024c) / UniTST (Liu et al, 2024b) / DeformTime (Shu and Lampos, 2024)
3) 시간 지연(Time Lags) 고려:
변수 간 관계에 시간 지연이 있을 수 있다는 점을 반영
-> 특정 변수의 변화가 다른 변수에 영향을 미치기까지 시간이 걸릴 수 있다는 점을 모델링
예: 기온과 전력 소비량: 오늘 기온이 급격히 올랐다면, 사람들이 에어컨을 가동하여 전력 소비량이 증가하는 데는 몇 시간 또는 하루 정도의 시간 지연 존재
VCformer (Yang et al, 2024b)
4.1.3 Exogenous Variable (외인성 변수)
- 내인성 변수(Endogenous Variable): 모델이 예측하려는 대상 자체의 과거 데이터(예: 특정 주식의 과거 가격)
- 외인성 변수(Exogenous Variable): 예측 대상에 영향을 미치지만, 예측 모델 자체에 의해 결정되지 않는 외부 변수 (예: 주식 가격 예측 시 관련된 경제 지표, 정치 변화).
외인성 변수를 통합하는 Transformer 기반 모델
TimeXer (Wang et al, 2024c)
-> 기존 Transformer 모델의 구조 변경 없이 외인성 변수를 통합하는 방법을 제안
TGTSF (Xu et al, 2024b)
-> 텍스트 데이터(채널 설명, 뉴스 메시지 등)를 외인성 변수로 활용하여 예측 정확도를 높임
4.1.4 Additional Approaches
일반화(Generalization) : 새롭고 이전에 보지 못했던 데이터에 대해서도 얼마나 잘 예측하는지
-SAMformer (Ilbert et al, 2024), Minusformer (Liang et al, 2024b)
다중 스케일(Multi-scale) : 시계열 데이터의 다양한 시간 스케일에서 정보를 추출하고 활용
-> 단기적인 변동성, 중기적인 계절성, 장기적인 추세 등 여러 스케일에서 고유한 패턴을 가질 수 있음
- Scaleformer (Shabani et al, 2023), Pathformer (Chen et al, 2024b)
디코더 전용(Decoder-only) : Transformer 에서 인코더 없이 디코더 부분만 사용하여 모델을 구성
-> LLaMA3와 같은 대규모 언어 모델(LLM)들이 인코더 없이 디코더만으로도 뛰어난 성능 -> TSF 적용
- LLaMA3 (Dubey et al, 2024), CATS (Kim et al, 2024)
특징 강화(Feature Enhancement) : 더 유용하고 효과적인 특징(feature)을 추출하거나 기존의 특징 학습 방식을 개선하여 예측 성능을 높임
- Fredformer (Piao et al, 2024): Basisformer (Ni et al, 2024)
4.2 Growth of Fundamental Deep Learning Models
- 4.2.1 MLP-Based Models
- 4.2.2 CNN-Based Models
- 4.2.3 RNN-Based Models
- 4.2.4 GNN-Based Models
4.2.1 MLP-Based Models
-> MLP의 구조적 한계(순차적 의존성 학습의 어려움, 긴 의존성 문제, 고차원 데이터 처리 및 주기적 패턴 포착의 한계)로 인해 관심이 줄었으나, 최근 연구에서 이러한 한계가 극복되고 뛰어난 성능 개선
N-BEATS (Oreshkin et al, 2020)
N-HiTS (Challu et al, 2023) - N-BEATS의 개선 모델로, 다변량(multivariate) 데이터를 처리
Koopa (Liu et al, 2024d
TSMixer (Ekambaram et al, 2023)
FreTS (Yi et al, 2024)
TSP (Wang et al, 2024e)
FITS (Xu et al, 2024c)
U-Mixer (Ma et al, 2024)
TTMs (Ekambaram et al, 2024)
TimeMixer (Wang et al, 2024a)
CATS (Lu et al, 2024)
HDMixer (Huang et al, 2024a)
SOFTS (Han et al, 2024), SparseTSF (Lin et al, 2024b), TEFN (Zhan et al, 2024)
PDMLP (Tang and Zhang, 2024), AMD(Hu et al, 2024b)
4.2.2 CNN-Based Models
-> 긴 시퀀스 내에서 다양한 지역적 패턴을 포착하는 CNN의 뛰어난 능력이 재평가되면서 다시 주목
3D Convolution: 복잡한 시공간(spatio-temporal) 시계열 데이터를 처리
-> 시간 축 뿐만 아니라 공간 또는 다차원 데이터를 동시에 처리
TimesNet (TimesNet), PatchMixer (PatchMixer)
TimesNet (Wu et al, 2023)
PatchMixer (Gong et al, 2023)
ModernTCN (Luo and Wang, 2024)
ConvTimeNet (Cheng et al, 2024b)
ACNet (Zhang and Wang, 2024)
FTMixer (Li et al, 2024d)
4.2.3 RNN-Based Models
Transformer 모델이 장기 시계열 데이터에서 보여준 한계점(예: 계산 복잡도, 긴 입력 길이에서의 성능 저하) 때문에, RNN은 시간 순서 학습을 효과적으로 활용하고 상대적으로 적은 데이터와 메모리로도 잘 작동한다는 장점으로 다시금 주목
실시간 스트리밍 데이터 처리
-> 모델이 전체 시퀀스를 한꺼번에 필요로 하지 않기 때문에(hidden state), 예측이 필요한 시점에 지연 없이 데이터를 처리
경량 모델이 필요한 환경
-> 모델 크기(메모리 사용량)가 시퀀스 길이에 비례하여 증가하지 않으므로, 제한된 메모리 환경에서 효율적
PA-RNN (Zhang et al, 2024c), WITRAN (Jia et al, 2024)
SutraNets (Bergsma et al, 2023), CrossWaveNet (Huang et al, 2024b)
DAN (Li et al, 2024c), RWKV-TS (Hou and Yu, 2024)
CONTIME (Jhin et al, 2024)
4.2.4 GNN-Based Models
-> 데이터 포인트 간의 복잡한 관계를 그래프 구조로 모델링하고 학습하는 데 강점
-> 특히 다변량 시계열 데이터의 복잡한 구조적 관계를 모델링하는 데 특화
그래프 구조 데이터의 증가
-> 최근 소셜 네트워크 등의 발전으로 많은 실세계 데이터가 자연스럽게 그래프 구조를 따르게 되면서 GNN의 적용 가능성이 확대
MSGNet (Cai et al, 2024a)
TMP-Nets (Coskunuzer et al, 2024)
HD-TTS (Marisca et al, 2024)
Fore-castGrapher (Cai et al, 2024b)
4.3 Emergence of Foundation Models
- 4.3.1 Sequence Modeling with LLMs
- 4.3.2 Pre-training
파운데이션 모델(Foundation Model)
-> 대규모 데이터로 사전 학습된 후 여러 특정 작업 및 도메인에 적용될 수 있는 모델
-> 다양한 작업과 도메인에서 뛰어난 성능과 강력한 제로샷(zero-shot) 능력을 보여주며 큰 주목
# 제로샷(Zero-shot) : 모델이 한 번도 본 적 없는 새로운 유형의 작업이나 클래스에 대해서도 추가적인 훈련 없이 추론하거나 예측할 수 있는 능력
기존 아키텍처 한계점
통계적 방법론, 전통적인 머신러닝, 딥러닝(MLP, CNN, RNN, GNN 등) 아키텍처
-> 귀납적 편향(inductive biases)으로 인해 성능에 제약
# 귀납적 편향(inductive biases) : 아키텍처 자체가 가지고 있는 특정 종류의 데이터나 패턴에 대한 선호, 가정
예) CNN: 이미지의 지역적 패턴에 강점, RNN: 시계열의 순차적 패턴에 강점
-> 파운데이션 모델은 특정 아키텍처의 고정된 귀납적 편향(inductive biases)에 갇히지 않고, 다양한 시계열 데이터와 태스크에 걸쳐 광범위하게 적용될 수 있는 더 강력한 일반화 능력 가짐
시계열 파운데이션 모델의 어려움
-> 시계열 데이터는 데이터셋에 따라 고유한 특성(예: 주기성, 트렌드, 비정상성 등)을 보임
-> 범용적 파운데이션 모델을 구축하기 어려움
예) 금융 시계열과 기상 시계열은 매우 다른 패턴과 통계적 속성 가짐
2) 구조화된 정보의 부재
-> 자연어에는 문법과 어휘라는 명확한 구조가 있고, 이미지에는 픽셀이라는 일관된 단위가 있음
-> 시계열 데이터는 이러한 보편적인 구조가 부족하여 모델이 일반화된 의미론적 패턴을 학습하기 어려움
(시계열 데이터는 단순하게 시간순서에 따라 나열된 숫자 값의 의미를 가짐)
3) 대규모 표준 벤치마크 데이터셋 부족
-> NLP의 GLUE나 CV의 ImageNet과 같은 대규모의 표준화된 벤치마크 데이터셋이 시계열 분야에는 부족
3) 대규모 표준 벤치마크 데이터셋 부족
-> NLP의 GLUE나 CV의 ImageNet과 같은 대규모의 표준화된 벤치마크 데이터셋이 시계열 분야에는 부족
4.3.1 Sequence Modeling with LLMs
-> LLM(Large Language Models)이 자연어 처리(NLP) 분야에서 보여준 강력한 시퀀스 처리 능력을 시계열 예측에 적용하려는 움직임이 등장
-> LLM이 텍스트에서 학습하는 방식(패턴 인식, 장기 의존성 파악, 문맥 이해)이 시계열 데이터의 트렌드, 계절성, 불규칙성, 그리고 다양한 변수 간의 복잡한 관계를 파악하는 데 효과적으로 활용될 수 있다고 기대
Fine-tuning 예측 기반
- GPT4TS (Zhou et al, 2023)
- PromptCast (Xue and Salim, 2023): - 수치 시계열 시퀀스(numerical time series sequences)를 텍스트 프롬프트(text prompts) 형태로 변환하여 대규모 언어 모델에 입력
제로샷(zero-shot) 예측 기반
- LLMTime (Gruver et al, 2023) - 시계열 데이터를 숫자 형태의 문자열(string of numerical digits)로 인코딩하여 LLM이 처리할 수 있도록 함
- Time-LLM (Jin et al, 2024) - Patch Reprogramming 도입
4.3.2 Pre-training
-> 대규모 사전 훈련(pre-training)을 통한 시계열 파운데이션 모델(time series foundation models)
Lag-LLaMA (Rasul et al, 2024)
TimesFM (Das et al, 2024)
CHRONOS (Ansari et al, 2024)
Uni2TS (Woo et al, 2024)
PSTA (Zhou et al, 2024a)
TEMPO (Shen et al, 2024)
4.4 Advance of Diffusion Models
- 4.4.1 Effective Conditional Embedding
- 4.4.2 Time Series Feature Extraction
- 4.4.3 Additional Approaches
Diffusion Model -> 노이즈(Noise)에서 시작하여 점진적으로 데이터를 재구성하는 방식으로 작동하는 생성 모델(Generative Models)
초기 -> DALL-E2, Stable Diffusion, Imagen과 같은 모델을 통해 고품질 이미지 생성 분야에서 큰 성공
오디오 생성, 자연어 처리(NLP), 비디오 생성 등 다양한 분야에서도 뛰어난 성능

순방향 과정 (Forward Process) - 데이터에 점진적으로 노이즈를 추가
역방향 과정 (Reverse Process) - 모델은 노이즈 제거 네트워크(denoising network)를 학습하여, 무작위 노이즈에서 데이터를 생성하도록 훈련
-> 단순히 미래의 특정 값을 예측하는 것을 넘어, 과거의 복잡한 시간적 패턴을 학습하여 미래에 발생할 수 있는 다양한 데이터의 흐름(패턴) 시나리오들을 만들어내는 능력
Diffusion Model 의 시계열 예측(TSF)에서의 이점
불확실성 모델링
확산 모델은 순방향 및 역방향 과정을 통해 불확실성을 효과적으로 모델링 -> 예측 구간(prediction interval)
확률적 예측
단일 예측값 대신 여러 가능한 확률적 예측 결과(multiple possible prediction outcomes)를 제공함으로써 실제 세계의 불확실성을 반영
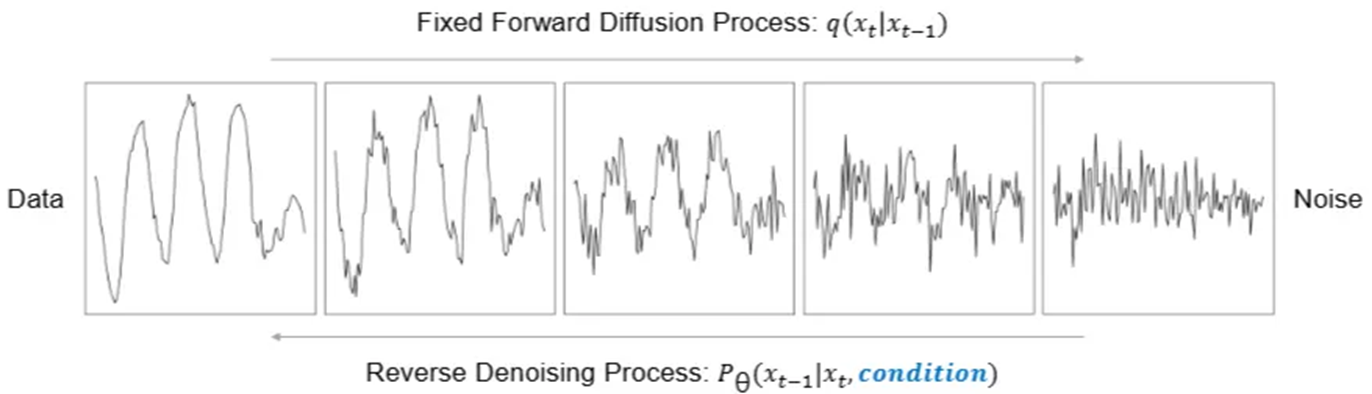
-> 노이즈를 추가했다가 제거하는 과정을 반복 학습하여, 데이터(historical data)를 조건으로 사용하여 모델이 미래 값을 학습하고 예측하도록 함
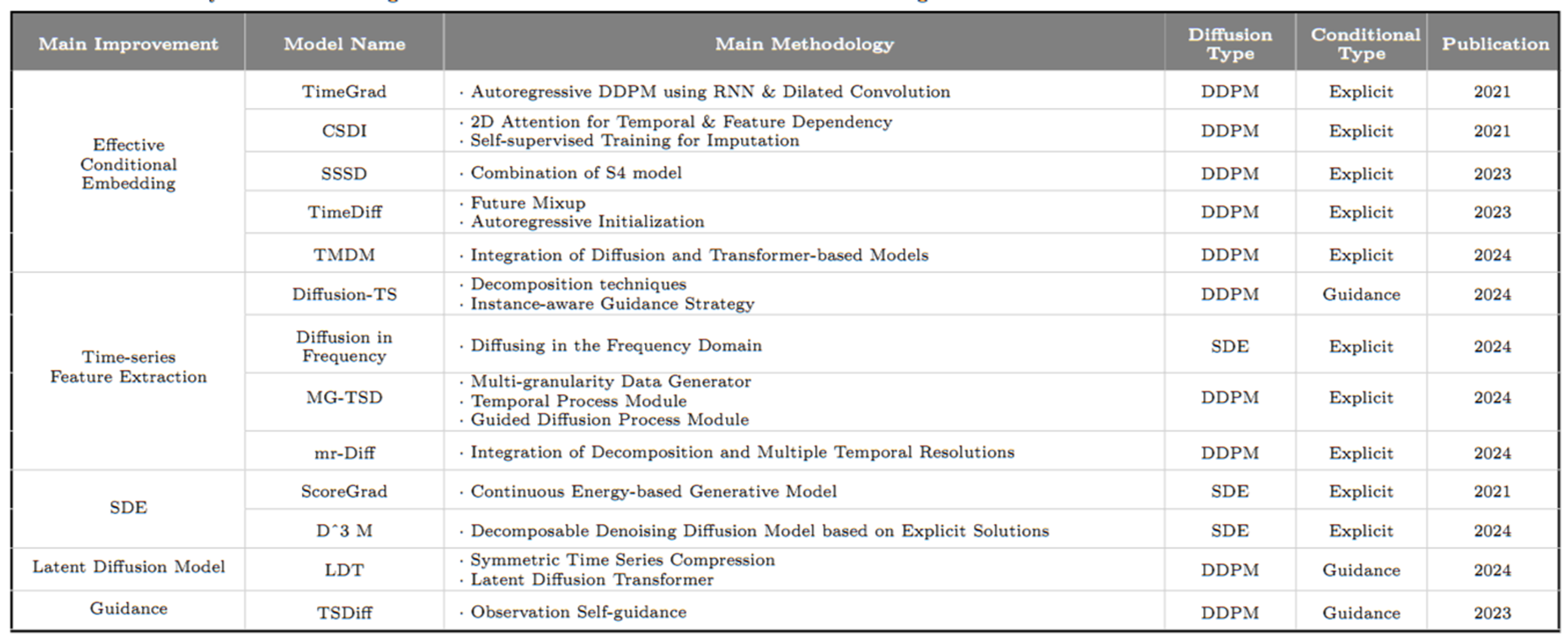
4.4.1 Effective Conditional Embedding
조건부 임베딩(Conditional Embedding) -> 과거 데이터를 모델이 효과적으로 이해하고 활용할 수 있도록 변환하는 과정
-> 역확산 과정(Reverse Denoising)이 미래를 예측할 때, 어떤 과거 정보를 '힌트'로 사용하는가
-> 단순히 과거 데이터를 있는 그대로 사용하는 것이 아니라, 예측에 필요한 핵심적인 정보(예: 트렌드, 계절성, 다변량 시계열 간의 관계 등)를 추출하고 압축하여 임베딩 형태로 제공
TimeGrad (Rasul et al., 2021)
CSDI (Tashiro et al., 2021)
SSSD (Alcaraz and Strodthoff, 2023)
TimeDiff (Shen and Kwok, 2023)
TMDM (Li et al., 2024b)
4.4.2 Time Series Feature Extraction
-> 시계열 데이터에서 미래 예측에 유용한 고유한 패턴(patterns), 트렌드(trends), 계절성(seasonality) 등의 특성을 찾아내고 분석 가능한 형태로 변환하는 과정
-> 원시 시계열 데이터는 복잡하고 노이즈(noise)를 포함하는 경우가 많기 때문에, 특징 추출(Feature Extraction)을 통해 모델이 학습하기 쉬운 형태로 데이터를 가공하여 예측 성능을 향상
Decomposition (분해): 시계열 데이터를 추세(trend), 계절성(seasonality),
불규칙성(irregularity)과 같은 구성 요소로 분해하여 각 구성 요소의 고유한 패턴을 분석
Diffusion-TS (Yuan and Qiao, 2024)
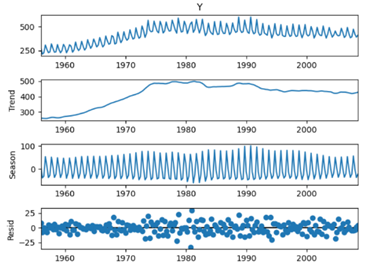
Frequency Domain (주파수 영역): 푸리에 분석(Fourier analysis)과 같은 분해 기법을 사용하여 시계열 데이터를 주파수 영역으로 변환하고 주기적인 구성 요소를 분석 - 주기적 패턴을 식별하고 노이즈를 제거하는 데 효과적
Crabbé et al. (2024)
Multi-Scale (다중 스케일): 다양한 시간 스케일(time scales - 초, 분, 시간, 일, 주, 월, 분기, 년)에서 시계열 데이터를 분석하여 장기적인 추세와 다양한 특징을 효과적으로 추출하는 기법
MG-TSD (Fan et al, 2024b), mr-Diff (Shen et al, 2024)
4.4.3 Additional Approaches
Score-Based Generative Modeling through Stochastic Differential Equations (SDEs) (Song et al, 2021)
기존의 Diffusion Model-> 노이즈를 추가하고 제거하는 과정을 이산적인(discrete) 시간 단계로 설명
SDEs-> 연속적인(continuous) 시간으로 일반화
Latent Diffusion Model
원본 데이터 공간이 아닌 잠재 공간(latent space)에서 확산(diffusion) 과정을 수행하도록 설계
Guidance
예측을 위해 Denoising 네트워크에 조건을 명시적으로 주입하는 대신, 모델의 샘플링 프로세스를 특정 방향으로 유도(가이드)하는 기법
4.5 Debut of the Mamba
State Space Model (SSM) - 상태공간모형
-> 시간에 따라 변화하는 시스템의 동적 상태를 모델링하는 수학적 프레임워크
-> 시계열 데이터와 같이 시간에 따라 변화하는 시스템의 내부 상태와 외부로부터의 입력, 그리고 관측되는 출력을 수학적으로 표현
RNN과 유사 - 관측 데이터와 은닉 상태 데이터를 결합하여 다음 상태를 예측 (과거 맥락에 따라 동적으로 반응)
-> 동적으로 계산됨
RNN과 차이 - 선형성(Linearity)과 시불변성(Time-Invariance, LTI) – 입력 시간에 따른 출력 변화 없음
-> 정적인 규칙대로 계산됨
Mamba(Gu and Dao, 2024) 새로운 아키텍처 등장 (Mamba: Linear-Time Sequence Modeling with Selective State Space (https://arxiv.org/abs/2312.00752)
Mamba 모델이 기존 State Space Models (SSMs)의 한계 극복
-> SSM의 고유한 순차 처리 능력을 유지하면서도 Transformer의 Attention 메커니즘이 가지는 장기 의존성 처리 능력과 유연성을 Selective SSM을 통해 결합 시도
5. TSF Latest Open Challenges & Handling Methods
-> TSF 분야가 현재 직면하고 있는 도전 과제(open challenges)들과 이를 해결하기 위한 다양한 접근 방식
5.1 Channel Dependency Comprehension
5.2 Alleviation of Distribution Shift
5.3 Enhancing Causality
5.4 Time Series Feature Extraction
5.5 Model Combination Techniques
5.6 Interpretability & Explainability
5.7 Spatio-temporal Time Series Forecasting
5.1 Channel Dependency Comprehension
채널 종속성 이해 (Channel Dependency Comprehension):
-> 여러 변수(채널) 간의 복잡한 상호 관계를 얼마나 잘 이해하고 활용하는지
CI (Channel Independence): 각 채널을 독립적으로 처리
CD (Channel Dependency): 채널 간의 상관관계를 모델링
-> 직관적으로는 채널 간의 관계를 고려(CD)하는 모델이 더 좋을 것 같지만, 최근 연구에서 각 채널을 독립적으로 처리(Channel Independence, CI)하는 간단한 모델(예: LTSF-Linear, PatchTST)이 더 좋은 성능
-> 현재의 모델들이 채널 간의 복잡한 관계를 효과적으로 학습하지 못하고 있다는 것을 시사
현실의 시계열 데이터는 학습할 때와 예측할 때의 패턴이나 분포가 변하는 경우가 많음
- 복잡한 CD 모델은 학습 시기의 채널 간 관계에 과도하게 적응(높은 capacity)하여, 실제 환경 변화에는 취약해짐 (낮은 robustness)
- 오히려 덜 복잡한 CI 모델은 채널 간 관계에 덜 의존하기 때문에, 환경 변화에 덜 민감하게 반응하여 더 안정적인 (높은 robustness) 예측 성능
-> 즉, 시계열 데이터의 특성과 불확실성을 고려할 때, 단순히 복잡한 모델(CD)이 항상 좋은 것이 아니라, 때로는 단순하고 견고한 모델(CI)이 더 나은 선택일 수 있음
5.2 Alleviation of Distribution Shift
Distribution Shift (분포 변화) 완화
-> Non-stationarity (비정상성) 초래
-> 전통적인 통계 모델이나 딥러닝 모델이 가정하는 '데이터 분포의 일정함'을 깨뜨림
-> 모델의 일반화(Generalization) 성능을 크게 저해
일반적인 분포 완화 기법
1) 도메인 적응 (Domain Adaptation)
모델이 학습한 데이터(소스 도메인)와 실제로 적용될 데이터(타겟 도메인)의 분포가 다를 때, 이 분포 차이를 줄여서 모델의 예측 성능을 높이는 기법
Maxi-mum Mean Discrepancy (MMD) (Wang et al, 2023a),
Generative Adversarial Networks (GANs) (Sankaranarayanan et al, 2018)
2) 전이 학습 (Transfer Learning) - Transfer Learning (Pan and Yang, 2009)
대규모의 관련 데이터셋으로 학습되어 많은 지식을 가지고 있는 모델(사전 학습 모델)을 가져와, 시계열 데이터셋이나 작업에 맞게 미세 조정(fine-tuning)하여 성능을 높이는 기법
3. 강건성 기법 (Robustness Techniques)
데이터에 포함될 수 있는 다양한 불확실성 요인 (예: 노이즈, 이상치, 데이터 부족, 잘못된 레이블 등)에도 불구하고, 모델의 예측 성능이 안정적이고 견고하게 유지되도록 만드는 기법
Dropout (Srivastava et al, 2014), Data Augmentation (Wong et al, 2016)
정규화-역정규화(Normalization-Denormalization) 프레임워크
-> 시계열 데이터 자체 내의 비정상성(Non-stationarity)을 직접적으로 다루기 위해 특화된 접근법
-> 목표: 모델이 데이터의 절대적인 스케일이나 시간에 따른 변화에 덜 민감하게 반응하도록 하여, 핵심적인 시간적 패턴 학습에 집중하도록 함
단계
1) 정규화 (Normalization) 단계 (모델 입력 전)
2) TSF 모델 예측 단계 (정규화된 데이터로)
3) 역정규화 (Denormalization) 단계 (모델 출력 후, 예측한 값)
DAIN (Passalis et al, 2019)
RevIN (Reversible Instance Normalization) (Kim et al, 2021) - TIME-LLM 도입
NST (Non-stationary Transformer) (Liu et al, 2022)
Dish-TS (Fan et al, 2023)
SAN (Statistical-Adaptive Normalization) (Liu et al, 2024e)
5.3 Enhancing Causality
인과 분석(Causal Analysis)
-> 데이터 패턴의 근본적인 요인 이해
-> 오해 가능성 있는 상관관계 방지 - 우연일치, 관찰되지 않은 제 3의 변수(교란변수, Confounding Variable)
-> 더 정확하고 견고한 예측
-> 모델의 해석 가능성 및 신뢰성 향상
Kuroshio Volume Transport (KVT) 모델 Qian et al. (2023)
-> 다변량 인과 분석(multivariate causal analysis)을 통해 인과 관계가 있는 변수만을 선택하고, 이를 LSTM 모델에 입력하여 예측을 수행
North Atlantic Oscillation 모델 Mu et al. (2023)
Causal-GNN (Wang et al., 2022b)
Caformer (Zhang et al., 2024b)
5.4 Time Series Feature Extraction
-> 모델 성능을 높이기 위해 시계열 데이터에서 유용한 정보를 뽑아내는 과정
- 5.4.2 Downsampling
- 5.4.3 Multi-scale
- 5.4.4 Domain transformation
- 5.4.5 Additional Approach

5.4.1 Decomposition(시계열 분해)
시계열 데이터를 추세(trend), 계절성(seasonality), 주기성(periodicity), 잔차(residual)와 같은 기본 구성 요소로 나눔 -> 본질적 패턴 파악 유용, 예측력 상승
이동 평균 커널(Moving Average Kernel) 활용
-> 시계열 데이터에서 일정 기간 동안의 평균값을 계산하여 데이터를 부드럽게 만드는(smoothing) 역할
-> 노이즈나 단기적인 변동이 제거되어 장기적인 추세가 더 명확하게 포착
-> 시계열 분해 과정에서 트렌드, 계절성 요소 추출시 이용
Autoformer (Wu et al, 2021), FEDformer (Zhou et al, 2022), LTSF-Linear (Zeng et al, 2023)
PDMLP (Tang and Zhang, 2024)
CrossWaveNet (Huang et al, 2024b), Leddam (Yu et al, 2024), Diffusion-TS (Yuan and Qiao, 2024)
5.4.2 Downsampling(다운샘플링)
-> 원본 데이터에서 데이터 포인트의 수를 줄이는 기법
-> 풀링(Pooling) 방법을 통해 구현 -> 시계열 데이터의 특정 구간에서 대표값을 추출
-> 데이터를 추세(trend) 성분과 주기(periodic) 성분으로 분리
# 풀링: 연속된 여러 데이터 포인트를 하나의 대표값으로 요약
ex) [10, 12, 9, 11, 20, 22, 19, 21] -> [10.5, 20.5] (각 4시점의 평균값)
cf) CNN – 풀링 레이어(Pooling Layer)
효과
고주파(High-frequency) 성분 억제: 풀링을 통해 단기적이고 불규칙한 노이즈나 변동성을 줄임
-> 빠르고 작은 변동들은 평균화되거나 상쇄
저주파(Low-frequency) 성분 강조: 장기적인 추세나 주기적인 패턴과 같은 중요한 정보를 부각
-> 느리고 큰 변화를 나타내는 성분들이 더욱 뚜렷하게 드러남
SparseTSF (Lin et al, 2024b), SutraNets (Bergsma et al, 2023)
5.4.3 Multi-scale
시계열 데이터를 단일한 시간 간격으로만 분석하는 것이 아니라, 다양한 시간 스케일(예: 시간별, 일별, 주별, 월별 등)에서 동시에 분석하여 패턴과 트렌드를 포착하는 방법
- 패칭(Patching) 기법 확장
-> 짧은 패치는 단기변동 패턴 포착, 긴 패치는 장기적인 트랜드 포착
MTST (Zhang et al, 2024e), PDMLP (Tang and Zhang, 2024), and FTMixer (Li et al, 2024d)
- 다중 스케일 분해(Multi-scale decomposition) -> 데이터를 여러 스케일로 분해
TimeMixer (Wang et al, 2024a), AMD (Hu et al, 2024b)
- 모델 아키텍처에 다중 스케일 적용
Scaleformer (Shabani et al, 2023) and Pathformer (Chen et al, 2024b)
- 계층적 시공간 다운샘플링(Hierarchical spatiotemporal downsampling)
HD-TTS (Marisca et al, 2024)
- 확산 모델(Diffusion models) -> 역확산 과정(diffusion reverse process) 다중스케일 도입
MG-TSD (Fan et al, 2024b) and mr-Diff (Shen et al, 2024)
5.4.4 Domain transformation
-> 데이터의 잠재된 주기적(periodic) 특성이나 다른 숨겨진 패턴을 더 효과적으로 파악하고 표현하기 위해 데이터를 다른 형태로 변환하는 기법
- Fourier transformation (푸리에 변환)
시계열 데이터를 여러 개의 주파수 성분(사인파와 코사인파)으로 분해하여 어떤 주파수가 데이터에 가장 강하게 존재하는지 보여줌
- Wavelet transformation (웨이블릿 변환)
푸리에 변환과 유사하게 주파수 성분을 분석하지만, 시간에 따른 주파수 변화도 함께 파악할 수 있어 비정상성(non-stationarity)을 띠는 데이터에 더 적합할 수 있음
- Cosine transformation (코사인 변환)
이산 코사인 변환(DCT)과 같은 형태로 영상 및 오디오 압축에 주로 사용되지만, 시계열 데이터의 주파수 특징을 추출하는 데도 활용될 수 있음
주기성 추출 (Periodicity Extraction)
-> 시계열 데이터에서 특정 주기를 가지고 반복되는 패턴을 찾아내는 것
-> 주기적 요소를 활용하여 시계열 성능 향상
Autoformer (Wu et al, 2021), TimesNet (Wu et al, 2023), MSGNet (Cai et al, 2024a)
-> 중요하다고 판단되는 주파수들을 선별적(selective)으로 선택하므로 모든 잠재 정보를 포함하지 못할 수 있음
주파수 도메인 학습 (Training in the Frequency Domain)
-> 주기성 추출의 한계를 극복
-> 시계열 데이터를 주파수 도메인으로 변환한 후 모델을 직접 훈련시키는 접근 방식
-> 모든 잠재적 주파수 구성 요소를 균등하게 학습하여 중요한 정보를 놓치지 않도록 함
FreTS (Yi et al, 2024), FEDformer (Zhou et al, 2022), Fredformer (Piao et al, 2024)
FITS(Xu et al, 2024c), DERITS (Fan et al, 2024a), SiMBA (Patro and Agneeswaran, 2024b)
WaveForM (Yang et al, 2023a), FTMixer (Li et al,2024d)
5.4.5 Additional Approach
FTMixer (Li et al, 2024d) - 시계열 데이터의 시간 영역(Time Domain)과 주파수 영역(Frequency Domain)의 장점을 모두 활용하여 예측 성능을 높임
고차원 임베딩 (High-Dimensional Embedding)
-> 데이터의 본질적인 정보를 더 잘 포착하기 위해 고차원 표현(high-dimensional representations) 생성
-> 데이터 내에 숨겨진 패턴이나 여러 변수 간의 상호작용을 더 풍부한 형태로 모델에 전달
CATS (Lu et al, 2024)
SOFTS (Han et al, 2024)
BSA (Kang et al, 2024)
5.5 Model Combination Techniques
- 5.5.1Ensemble Models
- 5.5.2 Hybrid Models
-> 앙상블: 여러 모델의 예측 결과를 나중에 합치는 것
-> 하이브리드: 여러 모델의 구조 자체를 통합하여 함께 작동하도록 만드는 것
5.5.1Ensemble Models
배깅 (Bagging, Bootstrap Aggregating) (Petropoulos et al, 2018)
-> 데이터를 무작위로 샘플링하여(부트스트랩 샘플링) 여러 독립적인 모델들을 학습시킨 후, 이 모델들의 예측 결과를 평균(회귀)하거나 투표(분류) 방식으로 결합
Kim and Baek (2022) - Wavelet 변환과 MLP 기반의 배깅 기법을 결합하여 단일변수 시계열 예측 성능을 개선

부스팅 (Boosting)
-> 모델들을 순차적으로 학습시키고 결합하는 방식
Gradient Boosting: (Friedman, 2001), XGBoost (Chen and Guestrin, 2016), LightGBM(Ke et al, 2017)
Liang et al (2024b) - 부스팅의 점진적 잔차 학습(residual learning) 방식을 딥러닝에 통합하여 시계열 예측을 향상시키는 연구
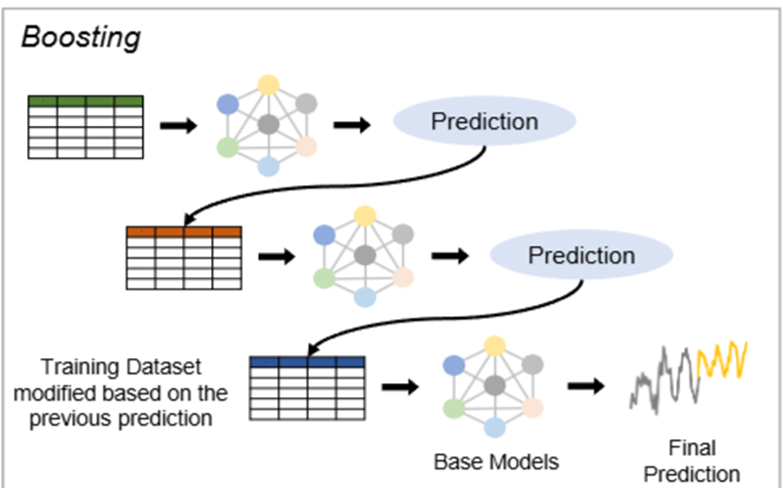
스태킹 (Stacking)
-> 여러 기본 학습기(base learners)의 예측 결과를 입력으로 받아, 이를 최종 예측을 생성하는 메타 모델(meta-model)에 학습
Massaoudi et al (2021) - LightGBM과 XGBoost를 스태킹하여 단기 전력 부하 예측의 불확실성을 다루고, 이 모델들이 생성한 메타 데이터를 MLP에 입력하여 최종 예측을 수행
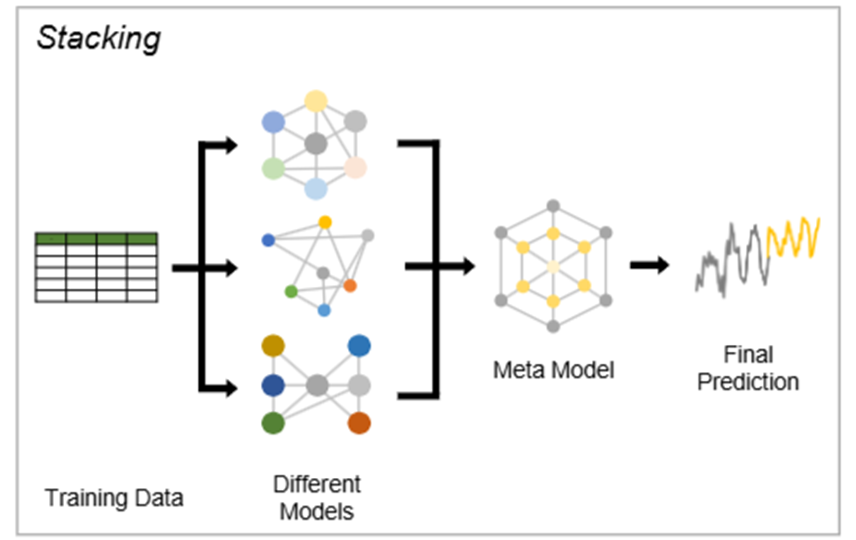
5.5.2 Hybrid Models
-> 서로 다른 유형의 모델이나 기술을 결합하여 각 모델의 강점을 활용하고 약점을 보완하는 접근 방식
ESRNN (Smyl, 2020) - 지수 평활(Exponential Smoothing, ES) + LSTM을 통합
TSLANet (Eldele et al, 2024) - (CNN + Transformer)
WaveForM (Yang et al, 2023a) - (웨이블릿 + GNN)
DERITS (Fan et al, 2024a) - (주파수 컨볼루션 + 시간 MLP)
BiTGraph (Chen et al, 2024c) - (TCN + GCN)
5.6 Interpretability & Explainability
Interpretability
-> 모델의 내부 작동 방식이나 의사결정 과정을 얼마나 쉽게 이해할 수 있는지
-> 모델 자체가 얼마나 투명한가
(예: 선형 회귀 모델, 의사결정 나무)
Temporal Fusion Transformer (TFT) (Lim et al, 2021)
Explainability (XAI)
-> 어떤 모델(특히 복잡한 블랙박스 모델)을 사용했든, 그 예측 결과를 사람이 이해할 수 있도록 ‘설명’
-> 모델의 출력을 설명하는 데 초점
(예: LIME, SHAP)
Ante-hoc Explainability (사전 설명 가능성)
-> 모델이 예측을 수행하기 전, 즉 설계 단계에서부터 모델의 동작 방식이 투명하여 쉽게 이해하고 설명할 수 있는 특징
-> 모델 자체가 투명하고 이해하기 쉬워서 설계 단계부터 설명이 가능한 경우
예) 선형 회귀(Linear Regression)나 의사결정 트리(Decision Trees)
Post-hoc Explainability (사후 설명 가능성)
-> 복잡한 모델, 특히 딥러닝 모델이 이미 훈련된 후에 해당 모델의 예측이나 의사결정 과정을 해석하고 설명
-> 복잡하고 불투명한 '블랙박스' 모델(예: 딥러닝 모델)의 예측을 설명하기 위해, 더 간단하고 해석 가능한 모델을 훈련하여 그 예측을 모방하고 설명하는 방법
2. Feature Attribution (특징 기여도) - SHAP (SHapley Additive exPlanations)
-> 각 입력 특징이 모델의 예측에 얼마나 기여했는지를 계산하여 특정 예측에 대한 입력 특징의 공헌도를 평가
3. Counterfactual Explanations (반사실적 설명)
-> 특정 예측을 변경하기 위해 어떤 입력값을 어떻게 변경해야 하는지를 설명
ForecastCF (Wang et al, 2023b)
5.7 Spatio-temporal Time Series Forecasting
시공간 시계열 예측(Spatio-temporal Time Series Forecasting)
-> 시간의 흐름에 따른 변화(temporal variations)뿐만 아니라, 특정 공간적 위치에서의 분포(spatial distributions)까지 동시에 포착
-> 즉, 데이터 포인트가 시간뿐만 아니라 공간 좌표도 함께 가지고 있으며, 이 두 가지 차원에서 모두 상호작용과 의존성을 가짐
-> 예시: 특정 도시 내 여러 센서에서 수집된 실시간 교통량 데이터, 여러 지역별 기온 변화, 특정 지역의 전염병 확산 추이 등
그래프 기반(Graph-Based) 방법
-> 공간적 관계가 있는 위치(노드)를 그래프의 노드로, 이들 간의 공간적 관계를 엣지(간선)로 표현, GCNs(Graph Convolutional Networks) 또는 그래프 기반 RNNs를 활용하여 공간적 의존성과 시간적 의존성을 동시에 학습
DCRNN [Li et al, 2018], ST-GCN [Yan et al, 2018], DB-STGCN [Li et al, 2024a]
래스터 기반(Raster-Based) 방법
-> 데이터를 2D 그리드(raster) 또는 비디오 형식으로 변환하여 공간적 위치와 시간적 패턴을 학습
ConvLSTM [Shi et al, 2015], ST-ResNet [Zhang et al, 2017], SLCNN [Zhang et al, 2020]
결합된(Combined) 접근 방식
GMAN [Zheng et al, 2020], STSGCN [Song et al, 2020], GCN-SBULSTM [Chen et al, 2021b]
'Paper review' 카테고리의 다른 글
| [Paper review] PatchTST (0) | 2026.01.30 |
|---|---|
| [Paper review] GAN(Generative Adversarial Nets) (0) | 2026.01.29 |
| [Paper review] DLinear (0) | 2026.01.12 |
| [Paper review] Prophet 톺아보기 (0) | 2025.12.07 |
| [Paper review] Time-LLM: Time Series Forecasting by Reprogramming Large Language Models (10) | 2025.07.16 |




