Hippo's data
[Paper review] GAN(Generative Adversarial Nets) 본문
오늘은 생성형 AI(Generative AI) 분야 고전명작 GAN이 제안된 논문에 대해 리뷰해보도록 하겠습니다!
Paper: Generative Adversarial Nets (Ian J. Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, Yoshua Bengio)
- Conference: NIPS 2014 (Neural Information Processing Systems)
- GitHub Repository: https://github.com/goodfeli/adversarial
- ArXiv: https://arxiv.org/abs/1406.2661
GitHub - goodfeli/adversarial: Code and hyperparameters for the paper "Generative Adversarial Networks"
Code and hyperparameters for the paper "Generative Adversarial Networks" - goodfeli/adversarial
github.com
Generative Adversarial Networks
We propose a new framework for estimating generative models via an adversarial process, in which we simultaneously train two models: a generative model G that captures the data distribution, and a discriminative model D that estimates the probability that
arxiv.org
1. SUMMERIZE
| 항목 | 핵심 내용 |
| Problem | 기존 생성 모델들 한계 → 기존의 생성 모델(RBM, DBM 등)은 복잡한 확률 분포를 근사하기 위해 다루기 힘든 확률적 가중치 계산이나 MCMC(Markov Chain Monte Carlo) 기법이 필요 → 이로 인해 고차원 데이터(이미지 등)를 생성시 계산 비용이 크고 효율성이 떨어짐 |
| Motivation | - 경쟁을 통한 발전: 모델을 두 개로 나누어 서로 경쟁하게 만들면, 명시적인 확률 밀도 함수 정의 없이도 데이터를 생성할 수 있음 - 예) 위조지폐범, 경찰: 생성자는 가짜를 진짜처럼 만들고, 판별자는 이를 잡아내려는 과정을 통해 자연스럽게 실제 데이터 분포를 학습 |
| Method | Adversarial Structure (적대적 구조) • Generator (G): 무작위 노이즈(z)를 입력받아 실제 데이터와 유사한 샘플을 생성 (판별자를 속이는 것이 목표) • Discriminator (D): 입력 데이터가 실제 데이터(X)인지 G가 만든 가짜인지 판별 (1=진짜, 0=가짜) • Minimax Game: 목적 함수를 통해 D는 최대화(정확도 향상), G는 최소화(오차 극대화)를 목표로 학습 minGmaxDV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]\min_{G} \max_{D} V(D, G) = \mathbb{E}_{x \sim p_{data}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))] |
| Results | 실험결과 • MNIST, TFD, CIFAR-10 데이터셋에서 기존 모델들보다 더 선명하고 그럴듯한 이미지 샘플을 생성함 • 이론적으로 학습이 완벽해지면 G는 실제 데이터 분포를 복제하며, D가 진짜와 가짜를 구분할 확률은 1/2(50%)에 수렴함을 증명 |
| Contribution | 생성 AI(Generative AI) 새로운 프레임워크 - 복잡한 추론이나 근사 없이 역전파(Backpropagation)만으로 생성 모델을 학습시킬 수 있는 프레임워크 제시 - 이후 DCGAN, StyleGAN 등 수많은 후속 연구의 토대가 됨 |
판별 모델(Discriminative Model) vs 생성 모델(Generative Model)
- 판별 모델 (Discriminative)
→ 클래스 간 결정 경계(Decision Boundary) 학습해서 예측 및 분류
- 생성 모델 (Generative)
→ 데이터 확률 분포 P(x)를 학습해서 새로운 샘플을 생성

생성 모델의 분류 체계 (Taxonomy)

→ 데이터 분포 P(x)를 모델이 어떤 방식으로 정의하고 학습하느냐
- 명시적(Explicit)
- 확률 분포 P(x) 수식으로 정의
- 수치를 최대화(Maximum Likelihood)하는 방향으로 학습
- 정확한 계산 (Tractable Density)
- 근사적 계산 (Approximate Density)
- VAE, Diffusion
- 암시적(Implicit)
- 확률 분포 P(x)를 명시적으로 정의하지 않음
- 실제 데이터와 유사한 샘플을 생성할 수 있는 확률 과정(Stochastic Process)을 학습하는 데 집중 (무작위 노이즈 → 정교환 데이터)
- GAN
2. DETAIL
기존 생성모델 한계
- RBM(제한된 볼츠만 머신), DBM(심층 볼츠만 머신) - 복잡한 계산 수식 필요
- 마르코프 체인 몬테카를로(MCMC) - 복잡한 샘플링 절차가 필요
→ 복잡한 계산, 샘플링 과정 필요없는 GAN(Generative Adversarial Nets) 방식 제안
Adversarial nets
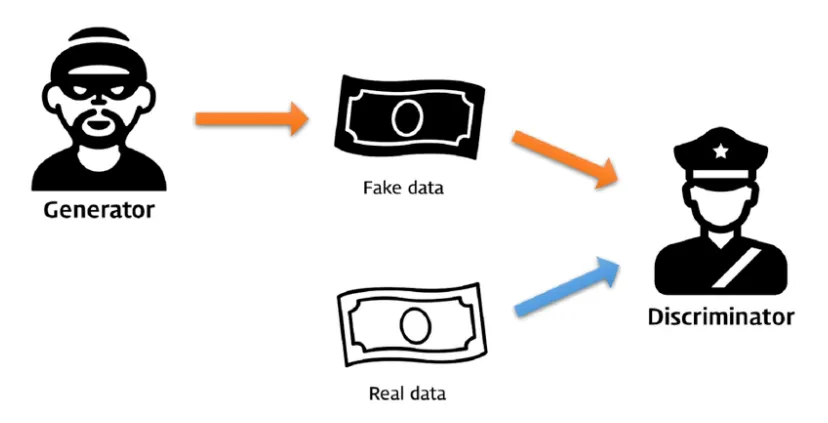
→ 두 모델(G,D)의 적대적 학습(Adversarial Training)을 통해 실제 데이터와 유사한 데이터를 생성
생성 모델 (Generator, G)
- 실제 데이터와 유사한 가짜 데이터(fake data) 생성 역할
- 위조지폐범
판별 모델 (Discriminator, D)
- 역할: 주어진 데이터가 실제 데이터(real data)인지, 생성 모델이 만든 가짜 데이터(fake data)인지 구분 역할
- 경찰
objective function
$min_Gmax_DV(D,G)=E_x∼p_{data}(x)[logD(x)]+E_z∼p_{z}(z)[log(1−D(G(z)))]$
- $\min_G \max_D V(D, G)$
- **G(생성자)**는 최소화(0.5 → 혼란) 목표
- **D(판별자)**는 최대화(1 = Real, 0 = Fake → 완벽한 판단) 목표
- $E_x∼p_{data}(x)[logD(x)]$: 첫번째 항 → 실제 데이터 입력
- $E_x∼p_{data}(x)$: 실제 데이터 분포( $p_{data}(x)$) 에서 추출된, 실제 데이터 x의 기댓값(expected value)
- $D(x)$: D(판별자) 출력
- D(판별자) 목표: 실제 데이터 x에 대해 D(x) = 1 목표
- $logD(x)$
- D(판별자) 관점: 최대화
- $D(x)$가 1에 가까워질수록 $log(1)$ = 0 (최대값)
- $D(x)$가 0에 가까워질수록 $log(0)$ = 음의 무한대(−∞) (최솟값)
- D(판별자) 관점: 최대화
→ 경찰(D, 판별자)의 판별능력
- $E_z∼p_{z}(z)[log(1−D(G(z)))]$: 두번째 항 → 가짜 데이터 입력
- $Ez∼p_z(z)$: 사전 노이즈 분포 $p_z(z)$에서 추출된 노이즈 샘플 $z$에 대한 기댓값(expected value)
- $D(G(z))$: G(생성자) 출력에 대한 D(판별자)의 출력
- D(판별자) 목표: 가짜 데이터 z에 대해 D(G(z)) = 0 목표
- G(생성자) 목표: 가짜 데이터 z에 대해 D(G(z)) = 1 목표
- $[log(1−D(G(z)))]$:
- D(판별자) 관점: 최대화
- G(생성자) 관점: 최소화
- $D(G(z))$가 0에 가까워질수록 $log(1)$ = 0 (최대값)
- D가 속지 않은 경우
- $D(G(z))$가 1에 가까워질수록 $log(0)$ = 음의 무한대(−∞) (최솟값)
- G(z)가 너무 진짜 같아서 D가 진짜라고 속은 경우
- $D(G(z))$가 0에 가까워질수록 $log(1)$ = 0 (최대값)
→ 경찰(D, 판별자)의 가짜 검거 능력
- $E_z∼p_{z}(z)[log(1−D(G(z)))]$: 두번째 항 → 가짜 데이터 입력
- $Ez∼p_z(z)$: 사전 노이즈 분포 $p_z(z)$에서 추출된 노이즈 샘플 $z$에 대한 기댓값(expected value)
- $D(G(z))$: G(생성자) 출력에 대한 D(판별자)의 출력
- D(판별자) 목표: 가짜 데이터 z에 대해 D(G(z)) = 0 목표
- G(생성자) 목표: 가짜 데이터 z에 대해 D(G(z)) = 1 목표
- $[log(1−D(G(z)))]$:
- D(판별자) 관점: 최대화
- G(생성자) 관점: 최소화
- $D(G(z))$가 0에 가까워질수록 $log(1)$ = 0 (최대값)
- D가 속지 않은 경우
- $D(G(z))$가 1에 가까워질수록 $log(0)$ = 음의 무한대(−∞) (최솟값)
- G(z)가 너무 진짜 같아서 D가 진짜라고 속은 경우
- $D(G(z))$가 0에 가까워질수록 $log(1)$ = 0 (최대값)
→ 경찰(D, 판별자)의 가짜 검거 능력
판별자(D) 최적점(Optimal Discriminator)
목표: 생성자(G)가 만들어낸 가짜 데이터 분포($P_g$)가 실제 데이터 분포($P_{data}$)와 완벽하게 일치
$P_g = P_{data}$
→ **판별자(D)**는 주어진 데이터가 (가짜, 실제) 어디에서 온건지 구별할 수 없게됨
→ 즉, **판별자(D)**가 내릴 수 있는 최선의 판단은 "모르겠다" 즉, 확률 0.5 (1/2)를 출력(완벽한 경우, Nash Equilibrium) 하는 것
$D^*G(x) = \frac{p{data}(x)}{p_{data}(x) + p_g(x)}$
- 만약 학습이 완벽하게 되었다면? ($P_g = P_{data}$)
- $D^*(x) = \frac{p_{data}(x)}{p_{data}(x) + p_{data}(x)} = \frac{1}{2}$
- 목적함수
- $\min_G \max_D V(D, G)$
- G를 고정, D를 먼저 최대화
- 판별자(D)의 성능이 좋은 상태에서, 생성자(G)의 성능을 올리는 것이 직관적임
$V(D, G) = E_{x \sim p_{data}(x)}[\log D(x)] + E_{z \sim p_z(z)}[\log(1 - D(G(z)))]$
$= \int_x p_{data}(x) \log(D(x)) dx + \int_z p_z(z) \log(1 - D(G(z))) dz$
$= \int_x p_{data}(x) \log(D(x)) + p_g(x) \log(1 - D(x)) dx$
기댓값 공식
|
(수식 단순화)
→ 적분 내의 수식을 최대화
함수 $y \rightarrow a \log(y) + b \log(1 - y)$ 가 있을 때, 이를 최대로 만드는 y값 = y 미분값 0
$f'(y) = \frac{a}{y} - \frac{b}{1-y}$
$\frac{a}{y} - \frac{b}{1-y} = 0$ (최댓값 = 0)
$\frac{a}{y} = \frac{b}{1-y} \Rightarrow a(1-y) = by \Rightarrow a = (a+b)y$
따라서, $y = \frac{a}{a+b}$
$D^*G(x) = \frac{p{data}(x)}{p_{data}(x) + p_g(x)}$
생성자(G) 최적점(Optimal Generator)
→ 판별자(D) 최적점(Optimal) 일때, 생성자(G) 손실함수
$C(G) = \min_G V(D, G)$
$V(D, G) = E_{x \sim p_{data}(x)}[\log D(x)] + E_{z \sim p_z(z)}[\log(1 - D(G(z)))]$
$D^*G(x) = \frac{p{data}(x)}{p_{data}(x) + p_g(x)}$ 대입,
$C(G) = E_{x \sim p_{data}} \left[ \log \frac{p_{data}(x)}{p_{data}(x) + p_g(x)} \right] + E_{x \sim p_g} \left[ \log \frac{p_g(x)}{p_{data}(x) + p_g(x)} \right]$
$C(G) = -\log(4) + E_{x \sim p_{data}} \left[ \log \frac{p_{data}(x)}{(p_{data}(x) + p_g(x))/2} \right] + E_{x \sim p_g} \left[ \log \frac{p_g(x)}{(p_{data}(x) + p_g(x))/2} \right]$
$C(G) = -\log(4) + KL \left( p_{data} \parallel \frac{p_{data} + p_g}{2} \right) + KL \left( p_g \parallel \frac{p_{data} + p_g}{2} \right)$ (기댓값 공식) (KLD 정의)
$C(G) = -\log(4) + 2 \cdot JSD(p_{data} \parallel p_g)$ (JSD 정의)
거리가 0이 되는 지점($p_g = p_{data}$)의 값
$C(G) = -\log(4) + 2 \cdot (0) = \mathbf{-\log(4)}$
| KL Divergence(Kullback-Leibler Divergence, KLD) → 두 확률 분포 사이의 차이를 측정하는 지표 → 실제 분포 $P$ 대신 우리 모델의 근사 분포(예측분포) $Q$를 사용했을 때 발생하는 정보의 손실 $P$ (True Distribution): 우리가 알고자 하는 정답 분포 $Q$ (Approximation): 우리가 모델로 만든 예측 분포
|
| JS Divergence(Jensen Shannon Divergence, JSD) → KLD 한계점: 방향에 따라 값이 다른 비대칭성 → 두 분포 $p$와 $q$사이의 거리를 잴 때, 중간 지점인 $M = \frac{p+q}{2}$를 활용 $JSD(p \parallel q) = \frac{1}{2} KL(p \parallel M) + \frac{1}{2} KL(q \parallel M)$
|
즉, 학습이 이상적으로 완료되었을 때 ($p_g = p_{data}$ )
→ 생성자 가짜데이터 분포가 실제 데이터 분포와 동일한 경우
- 판별자(D) 최적점 = 0.5 (진짜, 가짜 구별 못할 확률) → 직관과 동일
- 생성자(G) 최적점 = -log(4) = 약 -1.386 (가장 낮은 손실값) → 학습상 도달할 목표지점 존재
→ 목적함수의 정당성 입증
| 주의 $min_Gmax_DV(D,G)=E_x∼p_{data}(x)[logD(x)]+E_z∼p_{z}(z)[log(1−D(G(z)))]$ 수학적으로는 생성자(G) 학습시, $\log(1 - D(G(z)))$ 최소화하도록 학습하는 것이 맞지만, 실제 학습시 $\log(D(G(z)))$를 최대화하도록 변경 문제점 :
|

GAN 학습 과정
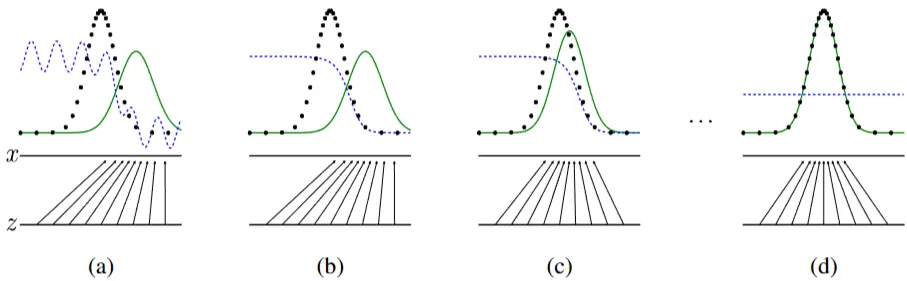
→ 단순한 분포$p_z(z)$에서 복잡한 실제 분포($p_{data}(x)$)로 변환해나가는 과정
- z: 간단한 분포(예: 균일 분포)에서 샘플링된 입력 노이즈
- x: $G(z)$에 의해 생성된 출력 샘플, 실제 데이터 공간
- 검은색 점선($p_{data}(x)$): 실제 데이터 분포(real, 학습해야 할 분포)
- 녹색 실선($p_g(x)$): G(생성자) 출력, 생성된 샘플의 확률분포(fake)
- 보라색 점선($D(x)$): D(판별자) 출력, 샘플 x가 실제 데이터 분포($p_{data}(x)$)에서 왔을 확률
(a) 훈련 초기
- 검정(real)과 녹색(fake) 분포가 전혀 다름
- G(녹색, 생성자)가 아직 실제와 유사한 샘플 생성하지 못함
- 검은색 점선이 높은 영역
- 보라점선 물결침 → D(판별자)가 실제, 가짜 구분 못함(판별경계 찾지 못한 상태)
(b) D(판별자) 학습
- D(보라) 판별자는 샘플을 정확하게 구별
- 검은색 점선이 높음 = 보라색 1(Real 판단)
- D(판별자)가 실제 데이터가 많은 부분을 진짜 데이터로 확신
- 녹색 실선 높음, 검은색 점선 낮음 = 보라색 0 (Fake 판단)
- D(판별자)가 실제 데이터가 적은 부분을 가짜 데이터로 확신
- 검은색 점선이 높음 = 보라색 1(Real 판단)
- 최적의 판별자($D^*_G(x)$)
- $D^*G(x) = \frac{p{data}(x)}{p_{data}(x) + p_g(x)}$
- $p_{data}(x)$: 실제 데이터 분포(real)
- $p_g(x)$: 생성자 분포(fake)
- 학습 목표: 내쉬균형(Nash Equilibrium)
- G(생성자)가 완벽하게 실제데이터를 만들어낸다면, =0.5 결과값 출력
- D(판별자)가 진짜, 가짜를 구분하지 못하는 상태
- $D^*G(x) = \frac{p{data}(x)}{p_{data}(x) + p_g(x)}$
(c) G(생성자) 업데이트
- 녹색(fake) 실선이 검은색 점선(real) 쪽으로 이동
- G는 D가 실제 데이터로 분류할 샘플을 생성하려고 노력 (하단 직선들)
(d)훈련 완료(수렴)
- 녹색 실선, 검은색 점선 일치 = 생성자(G)는 이제 실제 데이터와 구별할 수 없는 샘플을 생성가능
- 생성자(G)가 실제 데이터 분포를 학습
→ 최종적으로 진짜, 가짜 이미지를 구별할 수 없을 만한 데이터를 G가 생성
Experiments

- 노란색 상자: 각 행 우측 생성된 샘플과 가장 유사한 훈련(train) 샘플 이미지
→ 흑백, 컬러 등 다양한 유형 데이터에서 효과적으로 이미지 생성
→ 모델이 훈련세트를 단순히 암기(X), 유사하지만 분포가 다른 새로운 이미지 생성
Advantages and disadvantages
장점
- 간단한 훈련 과정: 마르코프 연쇄(Markov chain)나 복잡한 추론 과정 없이 역전파(back propagation) 사용하여 훈련, MLP 구조이므로 다양한 딥러닝 테크닉(dropout, RELU 등) 적용 가능
- 다양한 분포 표현 : 학습데이터를 직접 학습하는 것이 아니라, **생성자(G)**를 통해 피드백으로 학습하므로 다양한 이미지를 창의적으로 생성 가능
단점
- $p_g(x)$의 표현 어려움: G(생성자)를 통해 생성한 학습된 분포 $p_g(x)$를 특정한 수학적 공식(Explicit formula)으로 제시하지 못함
- G(생성자)를 통해 생성한 학습된 분포를 특정한 공식(Explicit)으로 표현하는 것이 아닌, 블랙박스 모델을 통해 생성한 결과(Implicitly)를 표현함
- Helvetica scenario(헬베티카 시나리오, = Mode Collapse) 문제
- 생성자(G)와 판별자(D) 학습이 균형을 이루지 못할 때
- 생성자(G)는 판별자(D)를 가장 쉽게 속일 수 있는 몇 가지 특정 패턴의 데이터만 반복적으로 생성
- 결국 **생성자(G)**는 다양한 무작위 입력(z)에도, 거의 똑같은 결과물만 출력
Future work
- 조건부 생성 모델 ($p(x|c)$)
- 기존 GAN:
- 입력 노이즈(z)만으로 이미지를 생성
- 원하는 조건의 이미지 생성 불가능
- MNIST(숫자 이미지 데이터셋)에서 어떤 숫자가 나올지 제어 불가
- 원하는 조건의 이미지 생성:
- Conditional GAN(cGAN) 사용
- Paper: Conditional Generative Adversarial Nets
- https://arxiv.org/abs/1411.1784
- 입력에 노이즈와 함께 조건(Label)을 추가
- 예시: label=3을 넣으면 3에 해당하는 숫자 이미지 생성
- 기존 GAN:
- stargan
- stylegan
- flow → AE - 완전복제가능
3. Implementation
https://github.com/goodfeli/adversarial/blob/master/show_samples.py
adversarial/show_samples.py at master · goodfeli/adversarial
Code and hyperparameters for the paper "Generative Adversarial Networks" - goodfeli/adversarial
github.com
mnist 데이터셋

출력 결과
- 학습 각 배치(batch)수별 결과 출력
- 학습이 진행될수록, 이미지 품질 좋아짐
0 → 10000 → 50000 → 90000

4. Questions
- 시계열(TS) 분야 생성 모델
- TimeGAN(Time-series Generative Adversarial Network) https://papers.nips.cc/paper_files/paper/2019/hash/c9efe5f26cd17ba6216bbe2a7d26d490-Abstract.html
- https://github.com/jsyoon0823/TimeGAN
Time-series Generative Adversarial Networks
Requests for name changes in the electronic proceedings will be accepted with no questions asked. However name changes may cause bibliographic tracking issues. Authors are asked to consider this carefully and discuss it with their co-authors prior to reque
papers.nips.cc
GitHub - jsyoon0823/TimeGAN: Codebase for Time-series Generative Adversarial Networks (TimeGAN) - NeurIPS 2019
Codebase for Time-series Generative Adversarial Networks (TimeGAN) - NeurIPS 2019 - jsyoon0823/TimeGAN
github.com
'Paper review' 카테고리의 다른 글
| [Paper review] PatchTST (0) | 2026.01.30 |
|---|---|
| [Paper review] DLinear (0) | 2026.01.12 |
| [Paper review] Prophet 톺아보기 (0) | 2025.12.07 |
| [Paper review] A Comprehensive Survey of Deep Learning for Time Series Forecasting: Architectural Diversity and Open Challenges (0) | 2025.11.25 |
| [Paper review] Time-LLM: Time Series Forecasting by Reprogramming Large Language Models (10) | 2025.07.16 |





