Hippo's data
[Paper review] DLinear 본문
오늘은 DLinear 모델이 제안된 논문을 리뷰해보도록 하겠습니다!
LTSF(Long term time-series Forecast) 분야에 굵직한 임팩트를 남겼던 논문인데욥
Transformer구조가 시계열 예측 분야에서 우세했던 상황에서 “ Transformer는 LTSF에 별로다” 라며 주장했던 논문입니다!
Paper: Are Transformers Effective for Time Series Forecasting? (Ailing Zeng, Muxi Chen, Lei Zhang, Qiang Xu)
- Conference: AAAI 2023
- GitHub Repository: https://github.com/cure-lab/LTSF-Linear
- ArXiv: https://arxiv.org/abs/2205.13504
Are Transformers Effective for Time Series Forecasting?
Recently, there has been a surge of Transformer-based solutions for the long-term time series forecasting (LTSF) task. Despite the growing performance over the past few years, we question the validity of this line of research in this work. Specifically, Tr
arxiv.org
1. SUMMARIZE
| 항목 | 핵심 내용 |
| Problem | 장기 시계열 예측(LTSF)에서 트랜스포머(Transformer)의 효과에 의문을 제기 → 복잡한 어텐션(Attention) 구조를 가진 트랜스포머 기반 모델들이 실제로 장기 예측 작업(LTSF)에서 효율적인지 |
| Motivation | 기존 트랜스포머 모델의 구조적 한계 지적 1. 순서 무시: Self-attention은 순서 불변(Permutation-invariant) 특성이 있어 시계열의 핵심인 '시간적 순서'를 보존하기 어려움. 2. 비효율적 복잡성: 모델은 매우 무겁지만, 실제 성능은 단순한 선형 결합보다 낮을 수 있다는 가설을 세움. |
| Method | LTSF-Linear (단순 선형 모델) • DLinear(Decomposition Linear) : 데이터를 추세(Trend)와 Reminder(Seasonal 등)으로 분해하여 각각 선형 학습 • NLinear(Normalization Linear): 데이터 분포 변화(Distribution Shift)를 막기 위해 입력값 정규화. (입력값에서 마지막 값을 빼서 정규화한 뒤 처리) |
| Results | SOTA 트랜스포머 모델 압도 ETT, Traffic, Electricity, Weather 등 9개의 벤치마크 데이터셋에서 MSE, MAE 지표 측정 Informer, Autoformer, FEDformer보다 훨씬 적은 파라미터로 20~50% 더 높은 성능 |
| Contribution | 시계열 예측 연구의 패러다임 전환 1. "무조건 복잡한 모델이 좋다"는 편향에 대적함, 시계열 데이터의 본질(추세/계절성)이 더 중요함을 입증 2. 향후 모든 시계열 연구에서 비교해야 할 강력하고 단순한 베이스라인(LTSF-Linear)을 제시 |
2. DETAIL
2-1. Introduction
최근 Transformer 기반 모델들이 LTSF에서 각광받고 있음
(LogTrans, Informer, Autoformer, Pyraformer, FEDformer 등)
Transformer의 강점: Transformer의 multi-head self-attention는 긴 시퀀스에서 의미 상관관계 추출하는 능력이 뛰어남 → NLP, CV, speech recognition 등 분야에서 탁월
시계열 분야의 한계: permutation invariant(순열 불변), anti-order→ 시계열 분야에 적합하지 않음
- permutation invariant → 시퀀스 순서 바뀌더라도 출력 영향 없음
- anti-order → 순서에 둔감
시계열 모델링에서는 데이터 포인트의 시간적 관계(temporal relations), 순서(order)가 중요
→ positional encoding, sub-series embedding → 순서 정보를 보존하려하지만 한계 존재
이에 LTSF-Linear 모델의 제안 및 Transformer와 비교
2-2. Preliminaries: TSF Problem Formulation
다중 스텝 예측 전략
- Iterated Multi-Step (IMS)
- 단일 스텝 예측 모델을 학습, 이 모델의 예측값을 다음 스텝의 입력으로 재사용하여 반복적으로(autoregressive) 여러 스텝을 예측하는 방식
- 장점: 예측값의 분산(variance)이 작음(autoregressive 추정) → 예측 결과가 안정적일 수 있음
- 단점: 예측 오차가 누적
- 적합한 경우: 정확한 단일 스텝 예측 모델이 있는 경우, 미래 예측 기간이 작을 때
- 단일 스텝 예측 모델을 학습, 이 모델의 예측값을 다음 스텝의 입력으로 재사용하여 반복적으로(autoregressive) 여러 스텝을 예측하는 방식
- Direct Multi-Step (DMS)
- 미래 스텝을 한 번에 예측
- 적합한 경우: 정확한 단일 스텝 예측 모델 아닌 경우(오차 누적될 수 있으므로), 미래 예측 기간이 길 때
- 미래 스텝을 한 번에 예측
2-3. Transformer-Based LTSF Solutions

Transformer-based TSF solutions Pipeline
- (a) Preproccessing - Time series decomposition (시계열 분해)
- Autoformer - seasonal-trend 분해
- moving average kernel 이용 → trend 추출
- (원본 - trend) = seasonal
- FEDformer - 다양한 커널 크기를 가진 이동 평균 → 다양한 추세 추출
- Autoformer - seasonal-trend 분해
- (b) Embedding
- 다양한 전략을 통해 시계열 입력에 시간적 맥락을 주입
- positional encoding, channel projection embedding, learnable temporal embedding
- (c) Encoder
- self-attention → O(L^2) 시간, 메모리 복잡도 (L : 시퀀스 길이)
- 복잡도 비효율성 해결위한 전략 제시
- sparsity(희소성) - 모든 요소 쌍을 고려하는 대신, 중요한 일부 요소 쌍에만 attention을 집중
- LogTrans, Pyraformer
- 저차원(low-rank) 특성 활용
- Informer, FEDformer
- Autoformer - auto-correlation 메커니즘 → 기존 self-attention 레이어 대체
- sparsity(희소성) - 모든 요소 쌍을 고려하는 대신, 중요한 일부 요소 쌍에만 attention을 집중
- (d) Decoder
- 기존 Transformer의 디코더는 → 자기회귀(autoregressive) 방식 → 느린 추론 속도, 오차 누적
- DMS(Direct Multi-Step, 한번에 여러 시점 예측) 위한 디코더 제안
- Informer - generative-style 디코더
- Pyraformer - 시공간 층 연결하는 fully-connected layer
- Autoformer, FEDformer - 분해(decomposition) 방식 도입
2-4. An Embarrassingly Simple Baseline
가설: 비-Transformer 모델들은 IMS 전략으로 평가, 이에 반해 기존 Transformer 기반 LTSF 모델의 뛰어난 성능은 DMS 전략을 사용했기 때문
→ IMS는 한 시점씩, 오차가 누적되어 평가되므로 장기예측 평가에 불리할 수 있음 (반면, DMS는 미래 시점을 한번에 예측)
가설 검증위해 LTSF-Linear 제안
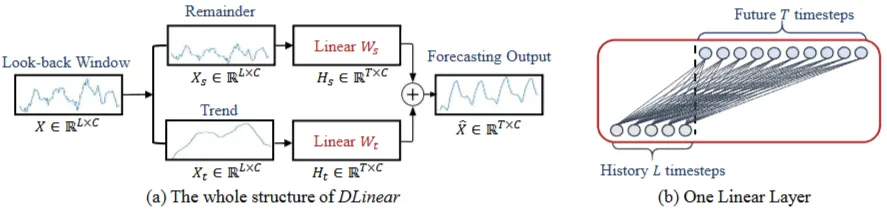
1) Linear (Vanilla Linear)
$\hat{X_i} = W X_i$
2) DLinear (Decomposition Linear)
→ 시계열 분해(Decomposition) 개념을 선형 모델에 접목
a. Moving Average(이동평균)를 이용해 데이터를 Trend(추세), Reminder(잔차) 성분으로 나눔
b. 각 성분 Linear 학습
c. 두 레이어의 결과를 합하여(Trend + Reminder) 최종 예측값 생성
$X^=Hs+Ht$
H_s: 잔차 성분(remainder series)으로부터 예측된 값
H_t: 추세 성분(trend series)으로부터 예측된 값
$H_s = W_s X_s$
- X_s: X에서 추세 성분 X_t를 뺀 잔차(reminder) 시계열
$H_t = W_t X_t$
- X_t: 이동 평균(moving average) 이용하여 분해된 추세
3) NLinear (Normalized Linear)
→ 분포 변화(Distribution Shift) 대응
정규화(Normalization): 입력 시퀀스의 마지막 값을 모든 시점의 값에서 빼줌
예)
실제 데이터: [1, 2, 3], 다음 숫자는 4
- 마지막 숫자 3을 모든 숫자에서 뺌: [1-3, 2-3, 3-3] = [-2, -1, 0]
- 정답 4에서도 3을 뺌: 4-3 = 1
→ 결론: 모델은 [-2, -1, 0]이 들어오면 1을 출력하도록 학습 (즉, 직전보다 1 커진다는 규칙(변화량)을 학습 )
실제 추론
실제 데이터: [100, 101, 102]
- 정규화: 각 숫자에서 마지막 값 102를 뺌
- [100-102, 101-102, 102-102] = [-2, -1, 0]
- 예측: [-2, -1, 0] → 1
- 복원: 1+102 = 103 (최종예측값)
2-5. Experiments
2-5-1. Experimental Settings
데이터 셋: 9개 다변량 시계열 데이터셋(ETT 계열 4종, Traffic, Electricity, Weather, ILI, Exchange-Rate)
평가 지표: MSE, MAE
비교방법:
- LTSF-Linear 모델, Transformer 기반 모델(5개 - FEDformer, Autoformer, Informer, Pyraformer, LogTrans) 비교
2-5-2. Comparison with Transformers
- 정량적 결과(Quantitative)
- LTSF-Linear는 기존의 복잡한 Transformer 기반 모델들을 모든 데이터셋에서 능가했으며, 종종 20%~50%에 이르는 상당한 성능 향상을 보임
- NLinear와 DLinear는 뚜렷한 분포 변화(train - test), 추세-계절성(trend-seasonality) 있는 데이터셋 처리에서 우수
- 정성적 결과(Qualitative)
- Transformer 기반 모델들이 Linear 모델에 비해 적절한 추세를 예측하지 못함
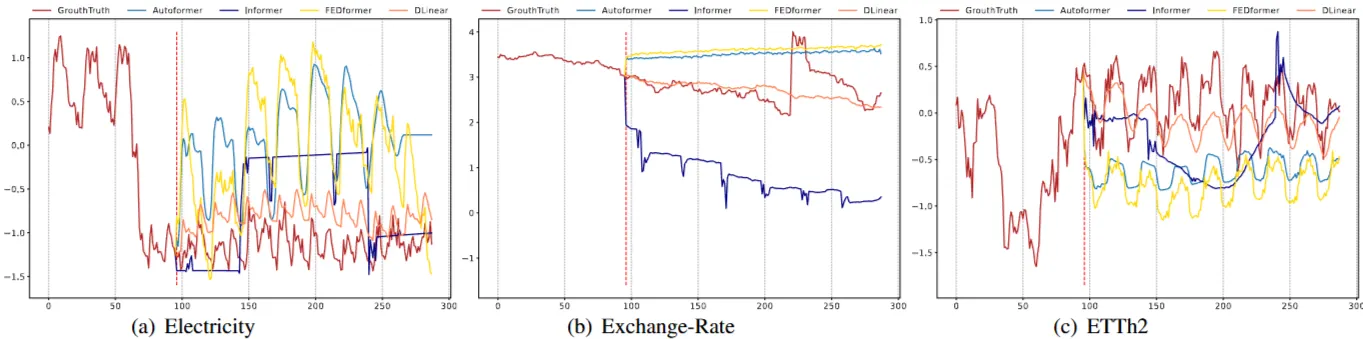
2-5-3 More Analyses on LTSF-Transformers
- 긴 입력 시퀀스에서 시계열 관계 추출 능력
- 가정: (시간적 관계를 잘 추출하는) 강력한 시계열 예측 모델은 더 많은 과거 데이터(더 큰 look-back window size)를 활용할 때, 예측 성능이 향상되어야 함
- 실험: look-back window size에 따른 성능 비교
- 결과:
- Transformer 기반: look-back window size가 증가해도 예측 성능이 저하되거나 안정적인 수준
- LTSF-Linear: look-back window size가 증가할수록 성능이 크게 향상
→ Transformer 모델들은 긴 시퀀스가 입력시, temporal noise에 과적합 경향
- 장기 예측에 중요한 요소
- 가설: 장기 예측은 시계열의 트렌드(trend)와 주기성(periodicity)을 얼마나 잘 포착하는지에 주로 의존
- 실험: 동일한 미래 시점을 예측할 때, 최근의 과거 데이터(Close)와 오래된 과거 데이터(Far)를 입력으로 사용했을 때의 Transformer 모델 성능을 비교
- 결과:
- Transformer 모델의 성능은 입력 데이터가 'Close'인지 'Far'인지에 따라 크게 변하지 않음
- Transformer가 시계열의 인접한 시간 정보를 활용하기보다는 데이터의 본질적인 특성(트렌드, 주기성 등)을 포착하려는 경향
- 오히려 본질적인 특성(추세, 주기성) 추출에는 많은 파라미터가 필요하지 않으니, 선형모델이 더 나을 수 있음
- Self-Attention 메커니즘의 효율성
- 실험: Informer 모델을 점진적으로 단순화하여 선형 모델로 변환
- Informer -> Attention-Linear(Self-Attention을 Linear로) -> Embed + Linear -> Linear
- 결과: 모델이 단순해질수록 Informer의 성능이 오히려 향상 (Self-Attention 등 복잡한 요소들이 불필요)
- 실험: Informer 모델을 점진적으로 단순화하여 선형 모델로 변환
- 시계열 순서 보존 능력
- 실험: 입력 시퀀스의 순서를 무작위로 섞거나(Shuf.) 절반을 교환하는(Half-Ex.) 방식으로 변화를 주어 모델 성능에 미치는 영향을 확인
- 결과:
- Transformer 기반: 성능에 큰 변동 없음 (시간 순서를 잘 보존하지 못함)
- LTSF-Linear: 입력 순서가 섞였을 때 성능 저하
- 다양한 임베딩 전략의 효과
- 실험: 위치 임베딩(positional embeddings), 타임스탬프 임베딩(timestamp embeddings)이 Transformer 기반 모델에 미치는 영향
- 결과:
- Informer- 위치 임베딩,타임스탬프 임베딩이 없으면 성능 감소
- FEDformer, Autoformer → 시퀀스 타임스탬프를 입력 (단일 타임스탬프 대신)
- 위치 임베딩 없어도 성능 유사
- 타임스탬프 임베딩 없으면 성능 감소
- 훈련 데이터 크기 제한
- 가설: Transformer 기반 모델의 저조한 성능이 벤치마크 데이터셋의 작은 크기 때문일 수 있음
- 실험: Traffic 데이터셋에서 전체 데이터셋(Ori.)과 단축된 데이터셋(Short)으로 훈련했을 때의 모델 성능을 비교
- 결과: 단축된 데이터셋으로 훈련했을 때 예측 오류가 더 낮은 경우 다수 → 훈련 데이터의 크기가 성능의 제한 요소가 아님
- 효율성 우선순위
- 가설: 바닐라 Transformer에 비해 개선된 Transformer(Informer, Autoformer, FEDformer 등)의 실제 추론 시간(inference time)과 메모리 비용이 개선되었는지
- 실험: DLinear, Transformer 모델들의 MACs (Multiply-Accumulate Operations), 파라미터 수, 추론 시간, 메모리 사용량을 비교
- 결과: 바닐라 Transformer와 비교했을 때, 대부분의 Transformer 변형 모델들은 실제 추론 시간, 파라미터 수가 비슷하거나 오히려 더 많음 → 오히려 개선되지 않음
2-6. 번외) 해석 관점
선형 레이어의 가중치 시각화
DLinear
미래 예측값에 대해 Trend / Reminder 부분 가중치 시각화
→ 예측된 미래 시점 y를 계산하는 데 사용되는 과거 시점 x의 가중치 값(W)
X축: 과거 입력 시점
y축: 예측할 미래 시점
보라 ~ 노랑(낮 ~ 높 가중치)
Exchange-Rate (c1)-(c8) - 금융 데이터는 일반적으로 계절성과 주기성이 부족
→ X축의 오른쪽(최근 과거 시점) 부분이 더 진하게 나타나는 경향(최근 시점 정보 큰 영향)

3. Implementation
LTSF-Linear 실험에 사용한 선형 모델 종류 3가지
https://github.com/cure-lab/LTSF-Linear/tree/main/models
LTSF-Linear/models at main · cure-lab/LTSF-Linear
[AAAI-23 Oral] Official implementation of the paper "Are Transformers Effective for Time Series Forecasting?" - cure-lab/LTSF-Linear
github.com
1. Linear (Vanilla Linear)
2. DLinear (Decomposition Linear)
3. NLinear (Normalized Linear)
individual 옵션에 따라 모든 채널(변수)이 하나의 가중치를 공유할지, 각 채널마다 별도의 Linear 레이어를 가질지 결정
- individual=True : DLinear-I (Individual Weights)
- → 변수별로 예측 방식이 다름
- → 논문에서 사용된 방식
- → 변수(채널)마다 별도의 Linear 레이어를 사용
- individual=False : DLinear-S (Shared Weights)
- → 모든 변수(채널)에 대해 하나의 Linear 레이어만 사용 = 가중치 행력이 모든 변수에 공통으로 적용됨
- → 변수 전체를 동시에 처리
- → default
예제 데이터 ETTh1 (Electric Transformer Temperature - Hourly 1)
데이터셋 Target: OT (Oil Temperature):
변압기의 오일 온도 외생 변수: - HUFL (High Use Full Load):
고압 사용처의 풀 부하량 - HULL (High Use Low Load):
고압 사용처의 저 부하량 - MUFL (Medium Use Full Load):
중압 사용처의 풀 부하량 - MULL (Medium Use Low Load):
중압 사용처의 저 부하량 - LUFL (Low Use Full Load):
저압 사용처의 풀 부하량 - LULL (Low Use Low Load): 저압 사용처의 저 부하량
Trend plot

EPOCHS = 10
LR = 0.01
seq_len: 168 (24*7)
입력 시퀀스 길이
pred_len: 168 (24*7)
예측 시퀀스 길이
enc_in: 7
입력 변수 개수(채널 수)
individual: True
변수별로 개별 Linear 레이어 사용 여부
모델 구조
Linear
Linear( (Linear): ModuleList( (0-6): 7 x Linear(in_features=168, out_features=168, bias=True) ))
NLinear
NLinear( (Linear): ModuleList( (0-6): 7 x Linear(in_features=168, out_features=168, bias=True) ))
DLinear
DLinear( (decompsition): series_decomp( (moving_avg): moving_avg( (avg): AvgPool1d(kernel_size=(25,), stride=(1,), padding=(0,))) )
(Linear_Seasonal): ModuleList( (0-6): 7 x Linear(in_features=168, out_features=168, bias=True) )
(Linear_Trend): ModuleList( (0-6): 7 x Linear(in_features=168, out_features=168, bias=True) ))


4. Questions
- LTSF-Linear는 정말 복잡한 패턴을 학습하는가, 아니면 단순히 평균적인 추세를 잘 따라가는 것인가? (변동성이 매우 큰 데이터에서도 선형 모델이 우위일지? - 예 : 코인 데이터)
- Transformer 계열 모델이 학습 데이터 양이 매우매우 많은 경우에는, 그럼에도 LTSF-Linear 모델이 우수할까? → (시계열 데이터 규모가 NLP 학습 수준처럼 매우 클 경우)
'Paper review' 카테고리의 다른 글
| [Paper review] PatchTST (0) | 2026.01.30 |
|---|---|
| [Paper review] GAN(Generative Adversarial Nets) (0) | 2026.01.29 |
| [Paper review] Prophet 톺아보기 (0) | 2025.12.07 |
| [Paper review] A Comprehensive Survey of Deep Learning for Time Series Forecasting: Architectural Diversity and Open Challenges (0) | 2025.11.25 |
| [Paper review] Time-LLM: Time Series Forecasting by Reprogramming Large Language Models (10) | 2025.07.16 |




