[TSF] Prophet 톺아보기

오늘은 2017년 2월에 메타(구 페이스북)에서 발표한 프로펫(Prophet) 모델에 대해 톺아보겠습니다!

해당 모델은 발표된지 꽤나 오래된 모델임에도 불구하고 시계열 예측 분야에서 아직까지도 많이 선호되는 모델인데요!!

왜 그런지 구체적으로 톺아보도록 하겠습니다!

최종적으로 BTC(비트코인) 데이터를 이용해서 간단히 실습해보도록 하겠습니다!

# Reference

 

Paper: Forecasting at Scale (https://peerj.com/preprints/3190.pdf)

공식 Doc: https://facebook.github.io/prophet/docs/quick_start.html

Quick Start

 

# 제안 배경

실제 비즈니스 현장의 복잡한 패턴 

- 강한 다중 계절성 (Multiple Strong Seasonalities): 주간 주기(weekly cycle), 연간 주기(yearly cycle) 

- 추세 변화 (Trend Changes): 시간에 따라 전반적인 방향 변화

- 이상치 (Outliers) 

- 휴일 효과 (Holiday Effects)

Facebook에서 생성된 이벤트 데이터 -> 다양한 복잡한 데이터 특징 존재함

 

 

기존 모델들의 한계

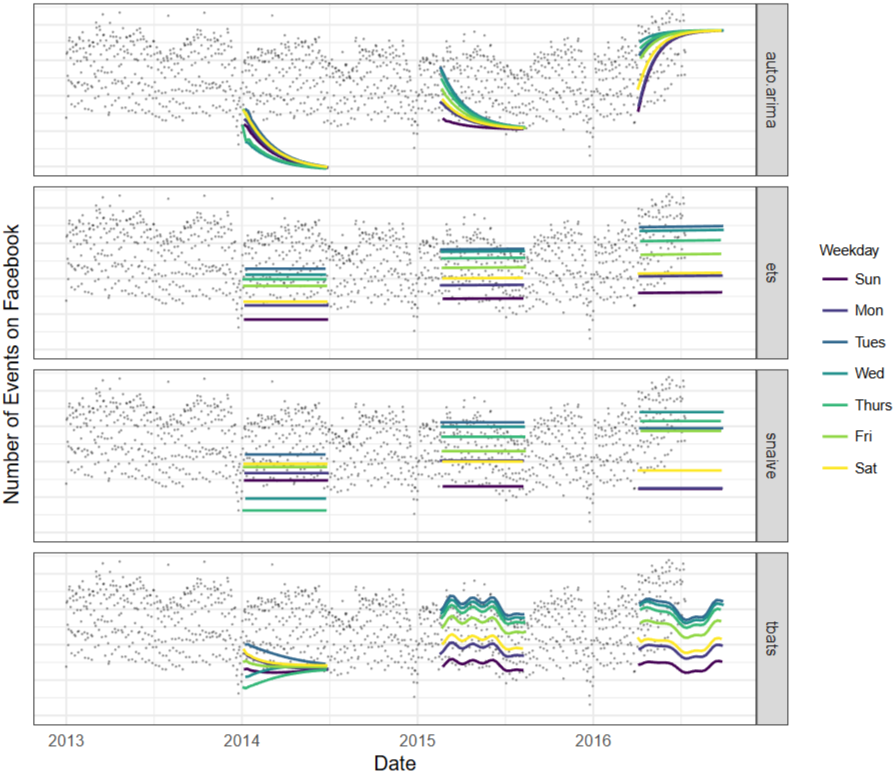
자동화된 예측 방법(automated forecasting procedures) - auto.arima, ets, snaive, tbats 
**  auto.arima -> AIC, BIC 에 따라 최적 파라미터 선정됨 / ets - >지수평활 모델중 최적 모델 자동으로 적용 / tbats -> 다중계절성 자동으로 탐지 등등

-> 기존 자동화된 예측 방법은 복잡한 시계열 데이터 예측을 잘 못하고 있음

 

한계점

-> 자동화되어 있지만, 복잡한 비즈니스 현장 데이터(예: 갑작스러운 추세 변화, 불규칙한 휴일 효과, 복잡한 계절성 패턴 등)의 특성을 반영하기 힘듦 

-> 예측 결과가 좋지 않을 때, 개선하기 위한 파라미터 조정이 어려움 (각 모델들의 작동방식을 이해해야함)

 

분석가 개입형(Analyst-in-the-Loop) 모델링 방식 제안 

 

-> 자동화된 부분(Automated) + 분석가 개입(Analyst-in-the-Loop) (시각적 검토, 도메인 지식 활용한 모델링)

 

# 수식 정리 

일반화 가법 모형(Generalized Additive Model, GAM)

-> 각 구성요소를 합(+)으로 분해, 각 요소가 미치는 영향을 정량적으로 분석

 

$y(t) = g(t) + s(t) + h(t) + \epsilon_t$

• $g(t)$ (Growth/Trend): 시계열의 전반적인 성장이나 하락 추세를 나타냄. 비주기적인 변화
• $s(t)$ (Seasonality): 연간, 주간, 일간 등 주기적으로 반복되는 패턴을 나타내는 계절성 함수
• $h(t)$ (Holidays): 휴일이나 특정 이벤트(예: 명절, 블랙 프라이데이, 공휴일 등)로 인해 발생하는 불규칙하지만 예측 가능한 효과

$t$ -> 시간, 시점

$y$ -> 타겟값

 

---

# 1. $g(t)$ (Trend)

두가지 모델로 구성됨

1) 포화 성장 모델 (Saturating Growth Model)

2) 구간 선형 모델 (Piecewise Linear Model)

 

1) 포화 성장 모델 (Saturating Growth Model)

-> S자 형태의 곡선 (수렴형)

-> 시장이 어느정도 한계점에 다다르면, 성장이 둔화되는 로지스틱 성장(Logistic Growth) 패턴 반영

$g(t) = \frac{C(t)}{1 + \exp(-k(t - m))}$

 

• $C(t)$ (Capacity): 최대 수용력 - 도메인 지식을 활용하여 직접 지정
  • C(t) -> 상수(C)가 아닌 시간에 따라 변하는 함수 C(t) 이용
  • 실제 비즈니스 환경을 유연하게 반영
• $k$ (Growth Rate): 성장의 속도를 나타내는 기울기(성장률)
• $m$: 곡선의 중심 위치를 결정하는 파라미터 ( g(t) = C/2가 되는 지점 -> m으로 정의하여 좌우이동)

 

코드

growth='logistic'

 

2) 구간 선형 모델 (Piecewise Linear Model)

포화 성장 X, 성장률이 구간별로 일정하게 유지되는 선형 모델

-> 전체 기간을 여러 구간으로 나누고, 각 구간마다 직선(Linear)을 그리는 방식

-> 여러 직선이 연결된 형태

 

$g(t) = \underbrace{(k + \mathbf{a}(t)^\mathsf{T} \boldsymbol{\delta})}_{\text{1. 현재 기울기}} t + \underbrace{(m + \mathbf{a}(t)^\mathsf{T} \boldsymbol{\gamma})}_{\text{2. 현재 절편}}$

 

$\mathbf{a}(t)$ : 변경점(Changepoint)이 지났는지 여부를 0,1로 표현

 

1) $(k + \mathbf{a}(t)^\mathsf{T} \boldsymbol{\delta})$ : 현재 기울기

• $\boldsymbol{\delta}$ (델타 벡터): 각 변경점마다 기울기가 얼마나 변하는지 저장된 벡터 $[\delta_1, \delta_2, ... \delta_S]^\mathsf{T}$
• $\mathbf{a}(t)^\mathsf{T} \boldsymbol{\delta}$: 두 벡터의 내적(Dot Product)
  • $\mathbf{a}(t)$에서 $1$인 부분(이미 지난 변경점)에 해당하는 $\delta$ 값들만 골라서 합산됨

 

2) $(m + \mathbf{a}(t)^\mathsf{T} \boldsymbol{\gamma})$ : 현재 절편

-> 선이 끊어지지 않게 $y$축 위치를 조정

 

 

코드

growth='linear' (기본값)

 

 

 

Logistic vs linear

 

 

 

# 2. $s(t)$ (Seasonality)

$s(t) = \sum_{n=1}^{N} \left( a_n \cos\left(\frac{2\pi n t}{P}\right) + b_n \sin\left(\frac{2\pi n t}{P}\right) \right)$

 

• $P$ (Period): 주기를 나타냄 / 연간 계절성은 $P=365.25$, 주간 계절성은 $P=7$을 사용
• $N$ (Fourier Order): 푸리에 항의 개수 - 모델의 복잡도 (계절성 패턴을 얼마나 세밀하게 표현할건지)
  • $N$ 값이 클수록 고주파(High-frequency) 변동까지 잡아내어 패턴이 복잡해지지만, 과적합의 위험이 증가
  • 논문에서는  연간 계절성에는 N=10, 주간 계절성에는 N=3을 기본값으로 추천
• an​,bn​: 각 주파수 성분(sine 및 cosine)의 진폭과 위상을 결정하는 계수

-> 계절성($N$) 개수에 따른 분해

-> 현재 이미지는 3개의 성분(N = 3)으로 분해

 

코드

m = Prophet(
    yearly_seasonality=20,  # '20'이 바로 N (기본값은 10)
    weekly_seasonality=5,   #  '5'가 바로 N (기본값은 3)
    daily_seasonality=True  # 'True'로 쓰면 기본값(N=4)이 적용
)

 

# 3. $h(t)$ (Holidays)

$h(t) = Z(t)\kappa$

 

• $Z(t)$ : 특정 날짜가 휴일인지 여부 나타냄(지시함수 Indicator function)
• $\kappa$ : 각 휴일의 영향력
  • holidays_prior_scale 파라미터 : $\kappa$의 정규화 강도를 조절하여, 특정 휴일이 전체 예측을 과도하게 왜곡하지 않도록 제어함
  • κ∼Normal(0,ν2) : 표준편차 v를 조절하며 휴일 효과를 조절

 

특정 국가의 휴일을 직접적으로 반영가능 (Python holidays 패키지에 의존하여 휴일 데이터를 가져옴)

https://github.com/vacanza/holidays

GitHub - vacanza/holidays: Open World Holidays Framework

-> 지원하는 국가, 휴일 확인

 

코드

# 1. 모델 생성 
m = Prophet()

# 2. 국가 공휴일 추가 (한국)
m.add_country_holidays(country_name='KR')

 

# 외생변수 추가

m.add_regressor('변수명')

-> 예측시, 미래 예측하려는 기간에 대한 정보도 알아야함 

 

# 코드 정리

from prophet import Prophet

 

모델생성

model = Prophet(...) 

 

추세(Trend)

파라미터명	기본값	설명 및 역할	사용 팁
growth	'linear'	성장 모델의 종류 'linear': 한계 없는 성장 (주가, 매출 등) 'logistic': 한계가 있는 성장 (인구, 서버 용량 등)	'logistic' 사용 시 데이터프레임에 cap (최대치) 컬럼이 필수로 있어야 함
changepoint_prior_scale	0.05	트렌드 유연성 조절 높음: 트렌드가 민감하게 변함 (과적합 위험) 낮음: 트렌드가 뻣뻣해짐 (과소적합 위험)	주가나 코인처럼 변동성이 심한 데이터는 0.1~0.5 정도로 값을 올려서 민감도를 높이는 것이 좋음
n_changepoints	25	변경점 후보 개수 트렌드가 꺾일 수 있는 지점(후보)을 전체 기간에 몇 개나 배치할지 결정	보통은 건드리지 않아도 됨. 데이터 기간이 매우 길다면 50 정도로 늘리는 것을 고려
changepoint_range	0.8	변경점 감지 범위 (비율) 데이터의 앞부분 몇 %까지만 보고 트렌드 변화를 학습할지 결정(기본값: 앞쪽 80%)	최근(데이터 끝부분)의 급격한 변화를 예측에 반영하고 싶다면 0.9~0.95로 늘려주세요.
changepoints	None	사용자 지정 변경점 (리스트) 모델이 자동으로 찾는 것 외에, 특정 날짜에 무조건 트렌드가 변한다고 강제할 때 사용	정책 변경일, 이벤트 발생일 등 명확한 날짜가 있을 때 ['2024-01-01', ...] 형태로 입력

 

계절성(Seasonality)

 

파라미터명	기본값	설명 및 역할	사용 팁
seasonality_mode	'additive'	계절성 결합 방식 'additive' (더하기): 계절성 진폭이 일정함 (예: 온도) 'multiplicative' (곱하기): 데이터 값이 커지면 계절성 진폭도 커짐 (예: 매출, 주가)	매출액이나 주가처럼 전체 덩치가 커질수록 변동 폭도 같이 커지는 데이터는 'multiplicative'가 적합
seasonality_prior_scale	10	계절성 반영 강도 높음: 계절 패턴을 아주 유연하게(강하게) 학습 낮음: 계절 패턴을 억제하여 일반화	계절성이 뚜렷하면 기본값을 유지하고, 과적합(너무 구불구불함)이 의심되면 값을 줄임
yearly_seasonality	auto (10)	연간 패턴 (N=10) 1년 주기의 패턴 유무 및 복잡도($N$) 설정	True로 설정 시 기본 복잡도 10이 적용 패턴이 매우 복잡하면 20
weekly_seasonality	auto (3)	주간 패턴 (N=3) 요일별(월~일) 패턴 유무 및 복잡도 설정	요일별 매출/방문자 차이가 확실하다면 True로 명시
daily_seasonality	auto (4)	일간 패턴 (N=4) 하루 중 시간대별 패턴 유무 및 복잡도 설정	시간(Hour/Minute) 단위 데이터가 아니라면(일별 데이터라면) False

 

 

이벤트 & 휴일 (Holidays)

파라미터명	기본값	설명 및 역할	사용 팁
holidays	None	휴일 정보 데이터프레임 반드시 holiday(이벤트명)와 ds(날짜) 두 개의 컬럼을 가진 DataFrame을 입력	명절뿐만 아니라 프로모션 기간, 신제품 출시일, 정책 변경일 등을 넣어 예측 정확도를 높일 수 있음
holidays_prior_scale	10	휴일 효과 반영 강도 높음: 이벤트 날짜에 예측값이 크게 뜀 (강한 영향) 낮음: 이벤트 효과를 보수적으로 반영 (약한 영향)	블랙프라이데이, 명절 등 매출이 폭발하는 초대형 이벤트가 포함되어 있다면 움

불확실성 & 통계적 추론 (Uncertainty)

파라미터명	기본값	설명 및 역할	사용 팁
interval_width	0.8	신뢰 구간 너비 예측값이 실제 발생할 확률 범위를 설정합니다. (기본값 0.8 = 80% 확률) 결과 그래프의 파란색 음영 영역 너비를 결정	리스크 관리가 중요한 비즈니스(재고 관리 등)에서는 0.95(95%)로 올려서 "최악의 경우"와 "최선의 경우" 범위를 넓게 보는 것이 안전
uncertainty_samples	1000	시뮬레이션 횟수 신뢰 구간(음영 영역)을 계산하기 위해 내부적으로 수행하는 몬테카를로 시뮬레이션 샘플링 횟수	기본값(1000)이면 충분 이 값을 너무 높이면 예측 속도가 불필요하게 느려짐
mcmc_samples	0	베이지안 추론 방식 (MCMC) 0: MAP 방식 (기본값) - 빠르고 근사치를 계산 정수(>0): MCMC 방식 - 매우 느리지만, 파라미터의 불확실성을 정밀하게 추정	데이터가 극도로 적거나, 예측값뿐만 아니라 파라미터 자체의 분포(불확실성)를 연구해야 할 때 사용(계산시간 수십배 늘어날 수 있음)

 

# 시각화

1. 기본 예측 그래프 (model.plot)

fig1 = model.plot(forecast)
plt.title(f"{ticker} Price Prediction")
plt.show()

• 검은 점 (Black Dots): 실제 관측 데이터 (Actual)
• 파란 실선 (Blue Line): 모델의 예측값 (yhat)
• 하늘색 영역 (Shaded Region): 신뢰 구간 (uncertainty_samples와 interval_width로 계산된 범위)

 

2. 요소 분해 그래프 (model.plot_components)

fig2 = model.plot_components(forecast)
plt.show()

 

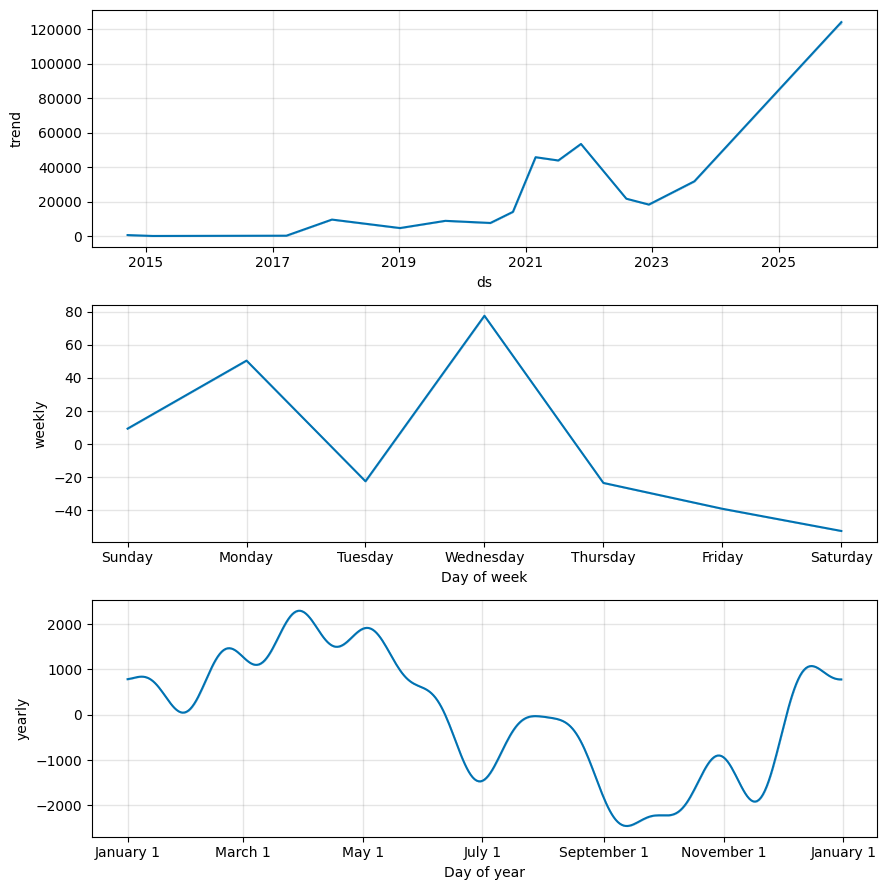
• Trend: 전체적인 우상향/우하향 추세
• Holidays: 휴일 효과가 있는 날짜의 스파이크(튀는 값)
• Weekly: 요일별 패턴 (월~일)
• Yearly: 연간 패턴 (1월~12월)
• Extra Regressors: (추가했다면) 외생변수의 영향력

 

3. 상호작용 그래프 (동적 Interactive 그래프 / Plotly 이용)

# 1. 동적 예측 그래프
fig3 = plot_plotly(model, forecast)
fig3.show()

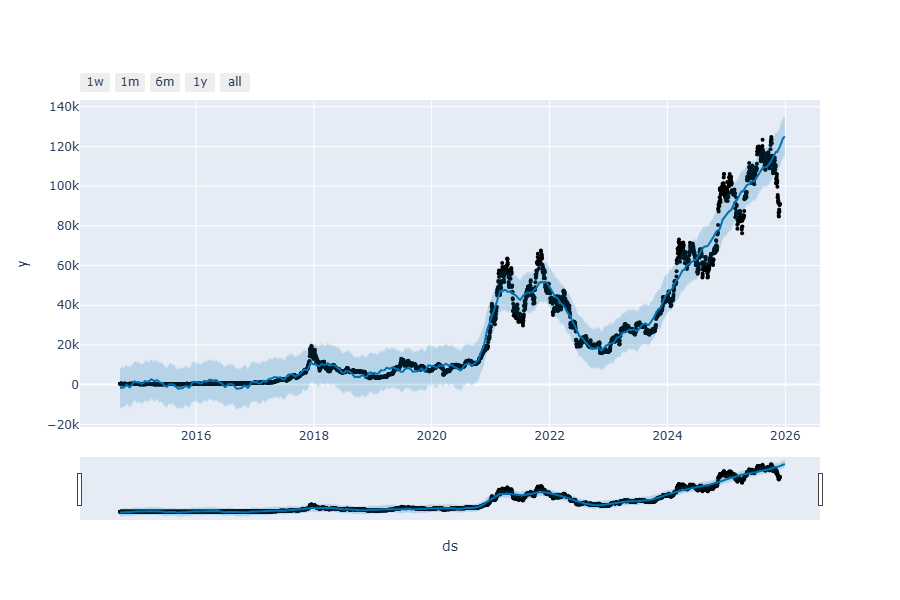
# 2. 동적 요소분해 그래프

from prophet.plot import plot_plotly, plot_components_plotly
fig4 = plot_components_plotly(model, forecast)
fig4.show()

# 교차검증 

 

일반적인 머신러닝의 랜덤 섞기(K-Fold)와 달리, 시간의 순서를 지키며 평가하는 방식 사용(Rolling)

예)

학습: 2025년 1월 검증: 2025년 2월 

학습: 2025년 2월 검증: 2025년 3월

학습: 2025년 3월 검증: 2025년 4월

from prophet.diagnostics import cross_validation, performance_metrics
from prophet.plot import plot_cross_validation_metric

# 교차 검증 실행 (오래 걸림)
df_cv = cross_validation(
    model, 
    initial='730 days',  # 초기 학습 기간 (최소 2년치 데이터로 시작)
    period='180 days',   # 테스트 반복 간격 (6개월마다 테스트)
    horizon='365 days'   # 예측 기간 (1년 뒤를 예측)
)
# 예측기간이 전체 데이터 개수를 넘기 전까지 진행

# 성능 지표 계산
df_p = performance_metrics(df_cv)

# 오차율(MAPE) 시각화
fig = plot_cross_validation_metric(df_cv, metric='mape')
# MSE, RMSE, MAE, MAPE, MDAPE(오차율 중간값)

 

# 교차검증 시각화 

from prophet.plot import plot_cross_validation_metric

# df_cv: cross_validation 함수 실행 결과로 나온 데이터프레임
# metric: 보고 싶은 오차 지표 ('mse', 'rmse', 'mae', 'mape', 'mdape' 중 선택)

# 예: MAPE(평균 오차율) 변화 그래프 그리기
fig = plot_cross_validation_metric(df_cv, metric='mape')

 

y축 : 오차지표

x축 : 예측 기간(며칠 뒤까지 예측했는지)

 

회색 점: 개별 검증 오차 (Individual Cross-Validation Metric)

- 기준 시점(Cutoff)으로부터 며칠 뒤를 예측했는가

- 과거 학습 기간은 반영X

 

파란 실선: 평균적인 오차 추세선 (Aggregated Metric Trend)

-> 보통 우상향(검증 기간이 길어질수록 오차 커짐)

-> 급격한 경사 -> 특정 기간 이후부터 오차가 폭발적으로 늘어남 -> 단기예측용

 

---

# 실습 (BTC 가격 예측)

일간으로 수집된 BTC 가격 -> 학습 2014-09-17 ~ 2025-10-31 / 검증 2025-11 (한달)

import yfinance as yf # 야후파이낸스 라이브러리 이용 -> 데이터 불러옴

import pandas as pd

from prophet import Prophet

import matplotlib.pyplot as plt

# ---------------------------------------------------------

# 1. 데이터 불러오기 (yfinance) / 2025-10-31까지 / 일간격

# ---------------------------------------------------------

ticker = "BTC-USD"

df = yf.download(ticker, period="max", end="2025-10-31", interval="1d")

 

비트 코인 가격을 df으로 가져옴

 

# ---------------------------------------------------------

# 2. 데이터 전처리 (Prophet 형식에 맞추기)

# ---------------------------------------------------------

# Prophet은 'ds' (날짜)와 'y' (타겟값) 두 개의 컬럼이 필요

df = df.reset_index()

# yfinance는 날짜에 시간대(timezone) 정보가 포함될 수 있어 제거(naive datetime)

# 시간대 정보

# 2023-12-07 09:00:00+09:00 → 한국 시간(UTC+9)

# 2023-12-07 00:00:00+00:00 → 영국 시간(UTC)

df['Date'] = df['Date'].dt.tz_localize(None)

# 종가(Close)를 예측 타겟으로

prophet_df = df[['Date', 'Close']].copy()

prophet_df.columns = ['ds', 'y']

 

프로펫 모델이 지원하는 df형식으로 변경(ds,y)

# ---------------------------------------------------------

# 3. 모델 학습

# ---------------------------------------------------------

model = Prophet(

    growth='linear',

    changepoint_prior_scale=0.1,

    seasonality_mode='additive',

    seasonality_prior_scale=10,

    holidays_prior_scale=10,

    daily_seasonality=False,

    weekly_seasonality=True,

    yearly_seasonality=True,

    interval_width=0.95,

    uncertainty_samples=1000

)

# 학습 시작

model.fit(prophet_df)

# ---------------------------------------------------------

# 4. 미래 예측 (Future Dataframe)

# ---------------------------------------------------------

# 학습 데이터 이후로 31일치의 미래 날짜를 자동으로 생성

future = model.make_future_dataframe(periods=31)

# 예측 수행

forecast = model.predict(future)

# 예측 결과 확인 (ds, yhat, yhat_lower, yhat_upper)

print(forecast[['ds', 'yhat', 'yhat_lower', 'yhat_upper']].tail())

 

# 교차검증

from prophet.diagnostics import cross_validation, performance_metrics

from prophet.plot import plot_cross_validation_metric

# 교차 검증: 2년 학습, 180일마다 30일 예측

df_cv = cross_validation(model, initial='730 days', period='180 days', horizon='30 days')

df_p = performance_metrics(df_cv)

# 성능 지표(MAPE 등) 출력

print(df_p[['horizon', 'mape', 'rmse', 'mae']].head())

# 성능 그래프 시각화

fig = plot_cross_validation_metric(df_cv, metric='rmse')

plt.show()

-> 평균적으로 1만 정도(달러, USD) 오차 

->BTC 예측은 쉽지않다,,,

 

# 외생변수 추가(S&P 500)

-> 미래 (S&P 500)값 안다고 가정 (현실에서는 해당 값도 예측해서 넣는 방식으로 동작 가능)

 

결과비교

-> 드라마틱하게 좋아지진 않는다,,,

Only 비트코인

RMSE:  $27,650.87
MAPE: 28.00%

 

비트코인 + S&P 500

RMSE (오차 금액): $13,852.70
MAPE (오차율)   : 14.07%

 

-> 다음 시간엔 프로펫 모델의 개선된 버전인 뉴럴 프로펫에 대해 톺아보겠따