Hippo's data
[Paper review] iTransformer 본문
오늘은 iTransformer 모델이 제안된 논문을 리뷰해보도록 하겠습니다!
기존 시계열 예측(TSF) Transformer 기반 모델의 대다수 방식이었던 기존 시간축 단위 토큰화에서 변수축 단위로 토큰화해서 어텐션 계산을 시도한 논문입니다!
ITRANSFORMER
Paper: ITRANSFORMER: INVERTED TRANSFORMERS ARE EFFECTIVE FOR TIME SERIES FORECASTING (Yongliu Liu, Tengge Hu, Haixu Zhang, Haoran Wu, Shiyu Wang, Maobing Ma, Jianmin Wang, Mingsheng Long)
- Conference: ICLR 2024
- GitHub Repository: https://github.com/thuml/iTransformer
- ArXiv: https://arxiv.org/abs/2310.06625
GitHub - thuml/iTransformer: Official implementation for "iTransformer: Inverted Transformers Are Effective for Time Series Fore
Official implementation for "iTransformer: Inverted Transformers Are Effective for Time Series Forecasting" (ICLR 2024 Spotlight) - thuml/iTransformer
github.com
iTransformer: Inverted Transformers Are Effective for Time Series Forecasting
The recent boom of linear forecasting models questions the ongoing passion for architectural modifications of Transformer-based forecasters. These forecasters leverage Transformers to model the global dependencies over temporal tokens of time series, with
arxiv.org
ITRANSFORMER = Inverted + TRANSFORMER
Inverted → 뒤바꿈, 반전
→ 기존 TRANSFORMER의 어텐션 계산이 시간축 단위였다면, 변수축 단위로 뒤바꿈
1. SUMMARIZE
| 항목 | 핵심 내용 |
| Problem | 기존 트랜스포머의 '토큰화' 방식의 부적절함 → 기존 모델은 동일 시점의 여러 변수(Multivariate)를 묶어 하나의 토큰으로 만듦 → 서로 다른 의미를 가진 변수들이 뒤섞이게 하고, 변수 간 상관관계를 학습하기 어렵게 함 |
| Motivation | 시계열 데이터의 특성 재해석 (Inverted) 1. 독립적 변수 특성: 각 변수는 고유한 패턴을 가짐. 시점 단위가 아니라 '변수 단로 정보를 추출해야 함 2. 어텐션의 역할 재정의: 시간 순서에 따른 어텐션보다, 변수들 사이의 관계를 파악하는 어텐션이 다변량 예측에서 더 효과적일 것이라는 가설 |
| Method | Inverted Structure (구조 뒤바꿈) • Variable as Token: 각 변수의 전체 시계열 데이터(Look-back window) 자체를 하나의 토큰으로 임베딩함 • Self-Attention: 변수 토큰들 간의 상호작용을 계산하여 변수 간 상관관계(Multivariate Correlation) 학습 • Feed-Forward Network (FFN): 각 변수 토큰 내의 시간적 패턴(Temporal patches)은 FFN을 통해 개별적으로 인코딩 |
| Results | 다변량 시계열 데이터에서 좋은 성능 • DLinear가 강점을 보였던 데이터셋뿐만 아니라, 변수 간 복잡한 관계가 중요한 데이터셋에서 DLinear를 능가 • Look-back window가 길어질수록 성능이 지속적으로 향상 (기존 트랜스포머는 성능이 정체되거나 하락했음) |
| Contribution | 트랜스포머 시계열 모델의 새로운 구조 제시 1. 구조 뒤바꿈 (inverted) 효과성: 복잡한 모듈 추가 없이, 데이터의 축(Time vs Variable)을 바꾸는 것만으로 트랜스포머의 한계를 극복 2. 범용성: 임베딩 방식만 바꾼 것이기에, 기존의 다양한 트랜스포머 변형 모델(Informer, Flowformer 등)에 즉시 적용 가능한 프레임워크 제공 |
2. DETAIL
1. Introduction

- Transformer, iTransformer 시계열 데이터 처리방식 비교
- Transformer
- Time Step 기준 토큰, 특정 시점의 모든 변수가 하나의 토큰에 포함됨
- 각 변수의 특징 학습 한계
- 무의미한 어텐션 맵(meaningless attention maps)
- 어텐션 → 시간 종속성(Temporal Dependencies) 파악 목적
- FFN(Feed foward network): 혼합된 토큰에서 시계열 특징 학습
- Time Step 기준 토큰, 특정 시점의 모든 변수가 하나의 토큰에 포함됨
- iTransformer
- 변수(Variate) 기준 토큰, 총 토큰의 수는 변수 개수
- 어텐션 → 변수간 상관관계(Multivariate Correlations) 파악 목적
- FFN(Feed foward network): 각 변수별 시계열 특징 학습
- Transformer
| Transforme | iTransformer (Inverted) | |
|---|---|---|
| 토큰의 의미 | 동일 시점의 변수 묶음 ($[v_1, v_2, \dots]$) | 한 변수의 전체 시계열($[t_1, t_2, \dots, t_L]$) |
| 어텐션 대상 | 시간(Time) 간의 상관관계 | 변수(Variate) 간의 상관관계 |
| FFN의 입력 | 시점별 다변량 벡터 | 변수별 전체 시계열 벡터 |
| FFN의 역할 | 변수 간 특징 추출 (Variate-Mixed) | 시간적 패턴 추출 (Variate-Unmixed) |
2. RELATED WORK
기존 Transformer 기반 시계열 예측 모델 분류

→ 구성요소(어텐션, Feed-forward network 등), 아키텍처(Transformer 구조) 수정 여부에 따라 4가지 범주로 구분 (modify the component and architecture)
- 구성요소(Component) 수정
- Transformer를 구성하는 각각의 부품을 수정하는 것
- 예) 기존 Attention을 효율적인 Sparse Attention으로 바꿈
- 아키텍처 (Architecture) 수정
- 기존 Transformer 구성 부품은 그대로, 부품을 조립하는 방식 변경
- 예) iTransformer: 기존 Attention은 시간관계 파악, inverted → 각 변수관계 파악
- 구성요소 수정 O, 아키텍처 수정 X
- 가장 일반적인 방식
- 어텐션 자체 수정(Sparse Attention 등)
- Autoformer, Informer
- 구성요소 수정 X, 아키텍처 수정 X
- 추가적인 시계열 처리(Series Processing) 도입
- Normalization, Patching 등
- PatchTST, NSTransformer
- 추가적인 시계열 처리(Series Processing) 도입
- 구성요소 수정 O, 아키텍처 수정 O
- Crossformer
- 구성요소 수정 X, 아키텍처 수정 O
- iTransformer
- 단치 각 구성요소 입력차원 inverted
- iTransformer
3. ITRANSFORMER
- historical observationsT : time steps
- N : variates
- $X = {x_1, \dots, x_T} \in \mathbb{R}^{T \times N}$
- predict the futureS: time steps
- N : variates
- $Y = {x_{T+1}, \dots, x_{T+S}} \in \mathbb{R}^{S \times N}$
Xt,: 특정 시간 스텝 t에서 동시에 기록된 모든 N개 변수의 값
X:,n: n번째 변수의 전체 시계열
3.1 STRUCTURE OVERVIEW
- iTransformer 전체 흐름
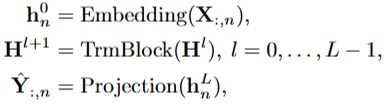
$\mathbf{h}_n^0$: n번째 변수의 전체 과거 시계열 X:,n을 *임베딩
*$\mathbf{H}^l$: $l$번째 트랜스포머 블록을 통과한 hidden state 행렬
$\hat{\mathbf{Y}}_{:,n}$: 번째 변수에 대한 최종 미래 예측값 (각 변수별로 미래 예측됨) / 최종적으로 선형레이어 통과(프로젝션)
- iTransformer 세부 구조 - encoder-only

(a) Embedding
- MLP(Multi-Layer Perceptron)
- 각 변수별로 전체 시계열을 Token으로 임베딩
(b) Multivariate Attention
- 각 변수별 임베딩된 토큰간 다변량 상관 관계(Multivariate Correlations) 포착
(c) Feed-forward Network(FFN)
- 각 변수별 독립적으로 적용
- 두 개의 선형 변환, 비선형 활성화 함수, 드롭아웃
- 시계열 특징 포착
(d) Layer Normalization
- 기존 Transformer: 각 시점 내에서 정규화
- iTransformer: 각 변수의 전체 시계열(Token)에 대해 정규화
- 비정상성(Non-stationarity) 해결에 도움
3.2 INVERTED TRANSFORMER COMPONENTS
Layer normalization

→ 각 변수에 대해 임베딩 (h_n)한 각 토큰을 독립적으로 평균이 0이고 분산이 1인 분포로 정규화
- 비정상 문제(non-stationary problem) 해결 효과적
- 비정상성(Non-stationarity): 시간에 따라 데이터 통계적 특성(평균, 분산)이 변함
- 기존 Transformer vs iTransformer
- 기존 Transformer
- 특정 시점(timestamp)의 다변량(multivariate) 데이터를 임베딩 →각 시간 토큰에 대해 정규화
- iTransformer
- 각 변수(variate)의 전체 시계열을 임베딩 → 각 변수 토큰에 대해 정규화
- 기존 Transformer
Feed-forward network (FFN)
$FFN(x)=max(0,xW1+b1)W2+b2$
→ 간단한 MLP 구조, 비선형성 학습(Relu 구조)
Self-attention
- 기존 attention
- 한 시점의 여러변수를 한 토큰으로 묶어서 어텐션 적용
- 시간적 의존성(temporal dependencies) 모델링
- iTransformer attention
- 각 변수 전체를 한 토큰으로 묶어서 어텐션 적용
- 변수간 상관관계 표현(multivariate correlation) - 밀접한 변수들에 더 높은 가중치 적용
4. EXPERIMENTS
4.1 FORECASTING RESULTS
Baselines
- 트랜스포머 기반: Autoformer, FEDformer, Stationary, Crossformer, PatchTST
- 선형 기반: DLinear, TiDE, RLinear
- TCN(Temporal Convolutional Network) 기반: SCINet, TimesNet
lookback length
- 96
prediction length
- PEMS 데이터셋: 12, 24, 36, 48
- 나머지: 96, 192, 336, 720
- 각 결과의 평균 MSE, MAE (전체 개별 예측값은 Appendix)
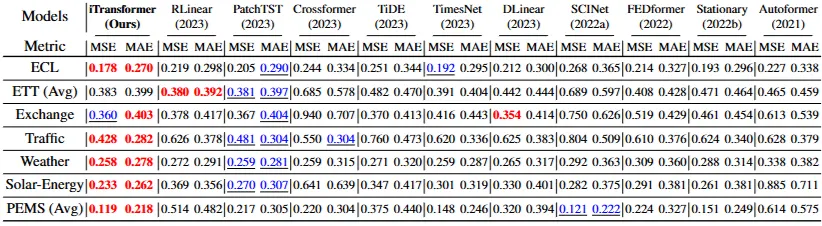
red: first best
blue: second best
results
- iTransformer SOTA
- 변동성 대처
- 기존 SOTA 모델 PatchTST 한계: PEMS 데이터셋과 같이 변동성이 심한 시계열에서 성능 저하
- iTransformer는 변동성에 잘 대처 (전체 시계열을 한 토큰으로 임베딩하므로)
- 다변량 상관관계 포착
- Crossformer 한계: 다변량 상관관계를 명시적으로 포착하는 모델 성능 떨어지는 경우 존재
- iTransformer는 변수간 상관성 포착에 강점 (변수별 토큰으로 어텐션 적용) → 고차원 데이터 뛰어남
- 변동성 대처
4.2 ITRANSFORMERS GENERALITY
Performance promotion
- 기존 Transformer 모델에 inverted 구조 적용
- 전체적으로 성능향상
- 기존 Transformer 아키텍처가 시계열 예측에 부적절하게 사용됨을 시사

Variate generalization

- 실험: CI-Transformers, iTransformer 간의 훈련 중에 보지 못한 시계열 변량(variates, 변수)에 대해 얼마나 잘 일반화되는지 성능 측정
- 결과: CI-Transformers 보다 iTransformer가 (100% → 20% variates 전환 시) 전반적으로 작은 예측성능 저하
- → iTransformer가 훈련에 보지 못한 변량에 대해 더 뛰어난 일반화 능력
- 이유:
- 기존 Transformer
- 특정 시점의 모든 변수를 묶어 시간적 토큰화(temporal token) → 토큰 개수 고정 (= input sequence 길이)
- Feed-Forward Network(FFN) → 시간적 토큰 독립적으로 적용 → 각 개별 변수의 시계열 패턴 포착 어려움
- iTransformer
- 각 변수의 전체 시계열 변량 토큰화(variate token) → 토큰 개수 유동적 (데이터 셋 변수 수에 따라 토큰 개수가 결정됨)
- 훈련, 추론단계 변수 수 달라져도 문제없이 동작 가능
- Feed-Forward Network(FFN) → 변량 토큰 독립적으로 적용 → 각 개별 변수의 시계열 패턴 포착 용이
- 기존 Transformer
Increasing lookback length

- lookback length: 48, 96, 192, 336, 720
- prediction length: 96
- 배경: 이전 연구(DLinear, PatchTST) 에서 lookback length가 늘어난다고 해서 예측성능이 반드시 늘어나지는 않음
- 기존 Transformer , inverted Transformer 의 성능 비교
- 기존 Transformer (채워진 도형) : lookback length 늘어나도 성능 오히려 악화되는 부분 존재
- inverted Transformer (구멍뚫린 도형) : lookback length 늘어날수록 성능 일관되게 향상됨
→ inverted 된 어텐션, FFN(MLP 구조)가 시간 관계를 잘 포착함을 시사
4.3 MODEL ANALYSIS
Ablation study
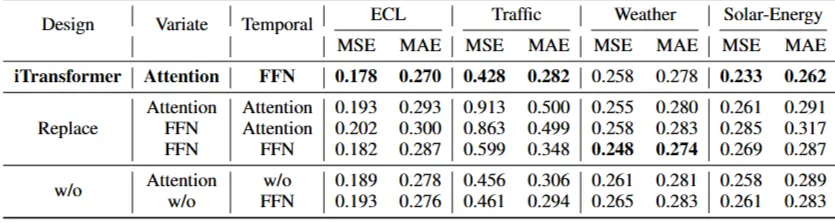
- 실험: 변수차원(Variate), 시점차원(Temporal) 각각 어텐션/FFN 구성요소 교체, 제거(w/o) 에 따른 성능 비교 실험
- 결과:
- iTransformer (변수 차원에 어텐션 사용, 시점 차원에 FFN사용) 구조 가장 우수한 결과
- 바닐라 Transformer (시점 차원에 어텐션 사용, 변수차원에 FFN사용) 구조 가장 최악 결과
- → inverted 방식 효과성 입증
Analysis of series representations & Analysis of multivariate correlations

(좌) MSE, CKA 유사성 비교
- CKA (Centered Kernel Alignment) 유사성: 두 신경망 계층이 학습한 표현이 얼마나 유사한지 측정하는 지표 (클수록 표현 유사성이 큼)
- CKA 유사성이 높을수록 더 정확한 예측으로 이어짐
- iTransformer가 일반 Transformer에 비해 더 높은 CKA 유사성 달성
(우) 다변량 상관관계 학습
- 목적: iTransformer에서 어텐션 메커니즘이 변수간 상관관계 학습을 잘하고 있는지 확인
- 실험: 각 변수간 실제 데이터(과거, 미래) 피어슨 상관관계 히트맵, 어텐션 스코어맵(첫번째, 마지막 레이어) 비교
- 결과: 각 레이어의 어텐션 스코어 맵이 실제 데이터의 상관관계 히트맵과 유사
- → 어텐션의 높은 해석 가능성, inverted 된 아키텍처가 다변량 상관관계 효과적을 포착
Efficient training strategy
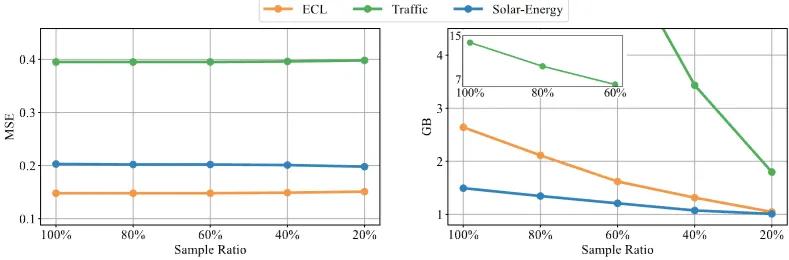
- 배경: Self-attention 메커니즘 복잡도 O(N^2) (N: 토큰 수) → 변수(variate) 수가 많을 경우 훈련 부담스러움
- 실험: 각 배치(batch)마다 일부 변수(variate)만 이용하여 학습 → 예측성능(MSE, 좌), 메모리(GB, 우) 비교
- iTransformer는 학습, 추론의 변수(토큰) 수가 동일하지 않아도 됨
- 결과:
- 학습 변량 비율(Sample Ratio) 감소하더라도 성능(MSE)이 안정적으로 유지
- 학습 변량 비율(Sample Ratio) 감소하더라도 메모리 사용량이 크게 감소
- → 학습 시, 일부 변량만 사용하여 효율성을 높임 / 추론 시, 모든 변량에 대해 예측을 수행
- 효과:
- 배치마다 변수 무작위 샘플링 → 일반화 효과 (특정 변수에 과하게 의존 방지)
- 메모리 효율성
3. Implementation
https://github.com/thuml/iTransformer
GitHub - thuml/iTransformer: Official implementation for "iTransformer: Inverted Transformers Are Effective for Time Series Fore
Official implementation for "iTransformer: Inverted Transformers Are Effective for Time Series Forecasting" (ICLR 2024 Spotlight) - thuml/iTransformer
github.com
TS shape
Raw Data [Time_steps, Variates] : 2차원
Input Tensor : 3차원
일반적인 구성: [B, L, N]
- B (Batch Size): 한 번에 학습할 샘플의 개수
- L (Look-back Window / Seq_Len): 모델이 과거를 얼마나 길게 보는지(입력 길이)
- N (Number of Variates): 변수 개수
* **iTransformer → [B, N, L] : 변수(N)를 토큰(Token)으로 취급하여 차원을 바꿈(Inverted)
-> 각 변수 전체 시계열은 압축되어 토큰화됨
-> 변수별 결측치(Missing Values), 시점 불일치(Misalignment) 등 불규칙한 데이터에도 별도의 전처리 없이 유연하게 적용 가능
4. Discussion
- 변수가 1~2개뿐인 경우의 성능? (Univariate vs. Multivariate)
- ***→ 어텐션 계산 유의미 → 단지 비선형 층을 통과하는 FFN(MLP) 모델과 동일할 가능성 큼
- iTransformer 한계
- FFN(feed-foward network)의 역할: 각 변수 상관관계 고려시, 변수별 거시적 패턴 학습
- 변수별 전체 시계열(Look-back Window)을 하나의 독립된 토큰으로 구성
- 한계: 시계열 전체를 하나의 토큰으로 보기 때문에, 특정 찰나의 순간에만 발생하는 미세한 변화 (시점별로 다른 변수의 상관관계)는 포착하기 힘듦
- → 제안: iTransformer (inverted) + Patching (관련해서 paper 있는지 찾아보기)
- 기존 iTransformer는 한 변수의 전체 길이를 하나의 토큰으로 만듦
- 기존 변수를 패치단위로 분할하여 여러 토큰으로 구성
- $토큰 수: N(변수 개수) \times P(패치 개수)$
- 시간 축(Patch)과 변수 축(Variate)을 나누어서 각각 어텐션 계산
'Paper review' 카테고리의 다른 글
| [Paper review] PatchTST (0) | 2026.01.30 |
|---|---|
| [Paper review] GAN(Generative Adversarial Nets) (0) | 2026.01.29 |
| [Paper review] DLinear (0) | 2026.01.12 |
| [Paper review] Prophet 톺아보기 (0) | 2025.12.07 |
| [Paper review] A Comprehensive Survey of Deep Learning for Time Series Forecasting: Architectural Diversity and Open Challenges (0) | 2025.11.25 |





